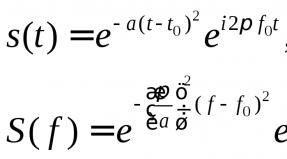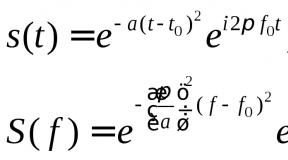Если плоская монохроматическая электромагнитная волна падает на свободную частицу с зарядом и массой , то частица испытывает ускорение и, следовательно, излучает. Направление излучения не совпадает с направлением падающей волны, частота же его при нерелятивистском движении совпадает с частотой падающего поля. В целом этот эффект можно рассматривать как рассеяние падающего излучения.

Мгновенное значение мощности излучения для частицы с зарядом при нерелятивистском движении определяется формулой Лармора (14.21):

где - угол между направлением наблюдения и ускорением. Ускорение обусловлено действием падающей плоской электромагнитной волны. Обозначая волновой вектор через к, а вектор поляризации -

через , запишем электрическое поле волны в виде

Согласно нерелятивистскому уравнению движения, ускорение равно

(14.99)

Если предположить, что смещение заряда за период колебания много меньше длины волны, то средний по времени квадрат ускорения будет равен При этом средняя мощность, излучаемая в единицу телесного угла, равна

Так как описываемое явление проще всего рассматривать как рассеяние, удобно ввести эффективное дифференциальное сечение рассеяния, определив его следующим образом:

Поток энергии падающей волны определяется средним по времени значением вектора Пойнтинга для плоской волны, т. е. равен . Таким образом, согласно (14.100), для дифференциального эффективного сечения, рассеяния получаем

Если падающая волна распространяется в направлении оси , а вектор поляризации составляет угол с осью как показано на фиг. 14.12, то угловое распределение определяется множителем

Для неполяризованного падающего излучения дифференциальное сучение рассеяния получается усреднением по углу , что приводит к соотношению

Это - так называемая формула Томсона для рассеяния падающего излучения на свободном заряде. Она описывает рассеяние рентгеновских лучей на электронах или у-лучей на протонах. Угловое

распределение излучения изображено на фиг. 14.13 (сплошная кривая). Для полного эффективного сечения рассеяния, так называемого томсоновского сечения рассеяния, получаем

Для электронов . Величина см, имеющая размерность длины, называется обычно классическим радиусом электрона, так как однородное распределение заряда, равного заряду электрона, должно иметь радиус такого порядка, чтобы собственная электростатическая энергия была равна массе покоя электрона (см. гл. 17).

Классический результат Томсона справедлив лишь на низких частотах. Если частота со становится сравнимой с величиной , т. е. если энергия фотона сравнима или превышает энергию покоя, то начинают существенно сказываться квантовомеханические эффекты. Возможна и другая интерпретация указанного критерия: можно ожидать появления квантовых эффектов, когда длина волны излучения становится сравнимой или меньше комптоновской длины волны частицы На высоких частотах угловое распределение излучения более сконцентрировано в направлении падающей волны, как показано пунктирными кривыми на фиг. 14.13; при этом, однако, сечение излучения для нулевого угла всегда совпадает с определенным по формуле Томсона.

Полное сечение рассеяния оказывается меньше томсоновского сечения рассеяния (14.105). Это так называемое комптоновское рассеяние. Для электронов оно описывается формулой Клейна - Нишины. Здесь мы приведем для справок асимптотические выражения

полного сечения рассеяния, определяемого по формуле Клейна - Нишины.

Формула Томсона названа в честь английского физика Уильяма Томсона , который вывел её в 1853 году , и связывает период собственных электрических или электромагнитных колебаний в контуре с его ёмкостью и индуктивностью .

Формула Томсона выглядит следующим образом :

$T\; =\; 2\backslash pi\; \backslash sqrt\{LC\}$

См. также

Напишите отзыв о статье "Формула Томсона"

Примечания

Отрывок, характеризующий Формула Томсона

– Да, да, знаю. Пойдем, пойдем… – сказал Пьер и вошел в дом. Высокий плешивый старый человек в халате, с красным носом, в калошах на босу ногу, стоял в передней; увидав Пьера, он сердито пробормотал что то и ушел в коридор.
– Большого ума были, а теперь, как изволите видеть, ослабели, – сказал Герасим. – В кабинет угодно? – Пьер кивнул головой. – Кабинет как был запечатан, так и остался. Софья Даниловна приказывали, ежели от вас придут, то отпустить книги.
Пьер вошел в тот самый мрачный кабинет, в который он еще при жизни благодетеля входил с таким трепетом. Кабинет этот, теперь запыленный и нетронутый со времени кончины Иосифа Алексеевича, был еще мрачнее.
Герасим открыл один ставень и на цыпочках вышел из комнаты. Пьер обошел кабинет, подошел к шкафу, в котором лежали рукописи, и достал одну из важнейших когда то святынь ордена. Это были подлинные шотландские акты с примечаниями и объяснениями благодетеля. Он сел за письменный запыленный стол и положил перед собой рукописи, раскрывал, закрывал их и, наконец, отодвинув их от себя, облокотившись головой на руки, задумался.

Tomsono virpesių formulė statusas T sritis fizika atitikmenys: angl. Thomson’s formula vok. Thomsonsche Schwingungsformel, f rus. формула Томсона, f pranc. formule de Thomson, f … Fizikos terminų žodynas

Зависимость дифференциального сечения рассеяния от угла рассеяния для различных значений энергий фотона Формула Клейна Нишины формула, описывающая … Википедия

- [по вмени англ. физика У. Томсона (W. Thomson; 1824 1907)] ф ла, выражающая зависимость периода Т незатухающих собственных колебаний в колебательном контуре от его параметров индуктивности L и ёмкости С: Т = 2ПИ корень из LC (здесь L в Гн, С в Ф … Большой энциклопедический политехнический словарь

Эффект Томсона одно из термоэлектрических явлений, заключающееся в том, что в однородном неравномерно нагретом проводнике с постоянным током, дополнительно к теплоте, выделяемой в соответствии с законом Джоуля Ленца, в объёме… … Википедия

Выражение для дифференц. сечения ds рассеяния фотона на электроне (см. Комптона эффект). В лаб. системе координат где частоты падающего и рассеянного фотона, элемент телесного угла для рассеянного фотона, угол рассеяния, параметр r0 = e … Физическая энциклопедия

- (Thomson) (в 1892 за научные заслуги получил титул барона Кельвина, Kelvin) (1824 1907), английский физик, член (1851) и президент (1890 1895) Лондонского королевского общества, иностранный член корреспондент (1877) и иностранный почётный член… … Энциклопедический словарь

- (Thomson, William), лорд Кельвин (1824 1907), английский физик, один из основоположников термодинамики. Родился в Белфасте (Ирландия) 26 июня 1824. Лекции отца, профессора математики университета Глазго, начал посещать уже в 8 лет, а в 10 стал… … Энциклопедия Кольера

I Томсон Александр Иванович , русский советский языковед, член корреспондент Петербургской АН (1910). Окончил Петербургский университет (1882). Профессор Новороссийского университета …

Томсон (Thomson), лорд Кельвин (Kelvin) Уильям (26.6.1824, Белфаст, ‒ 17.12.1907, Ларгс, близ Глазго; похоронен в Лондоне), английский физик, один из основателей термодинамики и кинетической теории газов, член Лондонского королевского общества (с … Большая советская энциклопедия

- (Thomson, Joseph John) (1856 1940), английский физик, удостоенный Нобелевской премии по физике 1906 за работы, которые привели к открытию электрона. Родился 18 декабря 1856 в пригороде Манчестера Читем Хилле. В возрасте 14 лет поступил в Оуэнс… … Энциклопедия Кольера

Формула Томсона:

Период электромагнитных колебаний в иде­альном колебательном контуре (т.е. в таком контуре, где нет потерь энергии) зависит от индуктивности катушки и емкости конденсатора и находится по формуле, впервые полученной в 1853 г. английским ученым Уильямом Томсоном:

Частота с периодом связана обратно пропорциональной зависимостью ν = 1/Т.

Для практического применения важно получить незату­хающие электромагнитные колебания, а для этого необходимо колебательный контур пополнять элек­троэнергией, чтобы скомпенсировать потери.

Для получения незатухающих электромагнитных колебаний применяют генератор незатухающих ко­лебаний, который является примером автоколеба­тельной системы.

См.ниже «Вынужденные электрические колебания»

СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ В КОНТУРЕ

ПРЕВРАЩЕНИЕ ЭНЕРГИИ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ

См.выше «Колебательный контур»

СОБСТВЕННАЯ ЧАСТОТА КОЛЕБАНИЙ В КОНТУРЕ

См.выше «Колебательный контур»

ВЫНУЖДЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ

ДОБАВИТЬ ПРИМЕРЫ СХЕМ

Если в контуре, в состав которого входят индуктивность L и емкость С, каким-то образом зарядить конденсатор (например, путем кратковременного подключения источника питания), то в нем возникнут периодические затухающие колебания:

u = Umax sin(ω0t + φ) e-αt

ω0 = (Собственная частота колебаний контура)

Для обеспечения незатухающих колебаний в состав генератора должен обязательно входить элемент, способный вовремя подключить контур к источнику питания, - ключ или усилитель.

Для того чтобы этот ключ или усилитель открывался только в нужный момент, необходима обратная связь от контура на управляющий вход усилителя.

Генератор синусоидального напряжения LC-типа должен иметь три основных узла:

Резонансный контур

Усилитель или ключ(на электронной лампе, транзисторе или другом элементе)

Обратную связь

Рассмотрим работу такого генератора.

Если конденсатор С заряжен и происходит его перезарядка через индуктивность L таким образом, что ток в контуре протекает против часовой стрелки, то в обмотке, имеющей индуктивную связь с контуром, возникает э. д. с., запирающая транзистор Т. Контур при этом отключен от источника питания.

В следующий полупериод, когда происходит обратная перезарядка конденсатора, в обмотке связи индуктируется э.д.с. другого знака и транзистор приоткрывается, ток от источника питания проходит в контур, подзаряжая конденсатор.

Если количество энергии, поступившей в контур, меньше, чем потери в нем, процесс начнет затухать, хотя и медленнее, чем при отсутствии усилителя.

При одинаковом пополнении и расходе энергии колебания незатухающие, а если подпитка контура превышает потери в нем, то колебания становятся расходящимися.

Для создания незатухающего характера колебаний обычно используется следующий метод: при малых амплитудах колебаний в контуре обеспечивается такой коллекторный ток транзистора, при котором пополнение энергии превышает ее расход. В результате амплитуды колебаний возрастают и коллекторный ток достигает значения тока насыщения. Дальнейший рост базового тока не приводит к увеличению коллекторного, и поэтому нарастание амплитуды колебаний прекращается.

ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА (уч.11кл.стр.131)

ЭДС рамки, вращающейся в поле

Генератор переменного тока.

В проводнике, движущемся в постоянном магнитном поле, генерируется электрическое поле, возникает ЭДС индукции.

Основным элементом генератора является рамка, вращающаяся в магнитном поле внешним механическим двигателем.

Найдем ЭДС, индуцируемую в рамке размером a x b, вращающейся с угловой частотой ω в магнитном поле с индукцией В.

Пусть в начальном положении угол α между вектором магнитной индукции В и вектором площади рамки S равен нулю. В этом положении никакого разделения зарядов не происходит.

В правой половинке рамки вектор скорости сонаправлен вектору индукции, а в левой половине противоположен ему. Поэтому сила Лоренца, действующая на заряды в рамке, равна нулю

При повороте рамки на угол 90о в сторонах рамки под действием силы Лоренца происходит разделение зарядов. В сторонах рамки 1 и 3 возникают одинаковые ЭДС индукции:

εi1 = εi3 = υBb

Разделение зарядов в сторонах 2 и 4 незначительно, и поэтому ЭДС индукции, возникающими в них, можно пренебречь.

С учетом того, что υ = ω a/2, полная ЭДС, индуцируемая в рамке:

εi = 2 εi1 = ωBΔS

ЭДС, индуцируемую в рамке можно найти из закона электромагнитной индукции Фарадея. Магнитный поток через площадь вращающейся рамки изменяется во времени в зависимости от угла поворота φ = wt между линиями магнитной индукции и вектором площади.

При вращении витка с частотой n угол j меняется по закону j = 2πnt, и выражение для потока примет вид:

Φ = BDS cos(wt) = BDS cos(2πnt)

По закону Фарадея изменения магнитного потока создают ЭДС индукции, равную минус скорости изменения потока:

εi = - dΦ/dt = -Φ’ = BSω sin(ωt) = εmax sin(wt) .

где εmax = wBDS - максимальная ЭДС, индуцируемая в рамке

Следовательно, изменение ЭДС индукции будет происходить по гармоническому закону.

Если с помощью контактных колец и скользящих по ним щеток соединить концы витка с электрической цепью, то под действием ЭДС индукции, изменяющейся со временем по гармоническому закону, в электрической цепи возникнут вынужденные электрические колебания силы тока – переменный ток.

На практике синусоидальная ЭДС возбуждается не путем вращения витка в магнитном поле, а путем вращения магнита или электромагнита (ротора) внутри статора – неподвижных обмоток, навитых на стальные сердечники.

Перейти на страницу:

• Электромагнитные колебания – это периодические изменения со временем электрических и магнитных величин в электрической цепи.

• Свободными называются такие колебания , которые возникают в замкнутой системе вследствие отклонения этой системы от состояния устойчивого равновесия.

При колебаниях происходит непрерывный процесс превращения энергии системы из одной формы в другую. В случае колебаний электромагнитного поля обмен может идти только между электрической и магнитной составляющей этого поля. Простейшей системой, где может происходить этот процесс, является колебательный контур .

• Идеальный колебательный контур (LC-контур ) - электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C .

В отличие от реального колебательного контура, который обладает электрическим сопротивлением R , электрическое сопротивление идеального контура всегда равна нулю. Следовательно, идеальный колебательный контур является упрощенной моделью реального контура.

На рисунке 1 изображена схема идеального колебательного контура.

Энергии контура

Полная энергия колебательного контура

\(W=W_{e} + W_{m}, \; \; \; W_{e} =\dfrac{C\cdot u^{2} }{2} = \dfrac{q^{2} }{2C}, \; \; \; W_{m} =\dfrac{L\cdot i^{2}}{2},\)

Где W e - энергия электрического поля колебательного контура в данный момент времени, С - электроемкость конденсатора, u - значение напряжения на конденсаторе в данный момент времени, q - значение заряда конденсатора в данный момент времени, W m - энергия магнитного поля колебательного контура в данный момент времени, L - индуктивность катушки, i -значение силы тока в катушке в данный момент времени.

Процессы в колебательном контуре

Рассмотрим процессы, которые возникают в колебательном контуре.

Для выведения контура из положения равновесия зарядим конденсатор так, что на его обкладках будет заряд Q m (рис. 2, положение 1 ). С учетом уравнения \(U_{m}=\dfrac{Q_{m}}{C}\) находим значение напряжения на конденсаторе. Тока в цепи в этом момент времени нет, т.е. i = 0.

После замыкания ключа под действием электрического поля конденсатора в цепи появится электрический ток, сила тока i которого будет увеличиваться с течением времени. Конденсатор в это время начнет разряжаться, т.к. электроны, создающие ток, (Напоминаю, что за направление тока принято направление движения положительных зарядов) уходят с отрицательной обкладки конденсатора и приходят на положительную (см. рис. 2, положение 2 ). Вместе с зарядом q будет уменьшаться и напряжение u \(\left(u = \dfrac{q}{C} \right).\) При увеличении силы тока через катушку возникнет ЭДС самоиндукции, препятствующая изменению силы тока. Вследствие этого, сила тока в колебательном контуре будет возрастать от нуля до некоторого максимального значения не мгновенно, а в течение некоторого промежутка времени, определяемого индуктивностью катушки.

Заряд конденсатора q уменьшается и в некоторый момент времени становится равным нулю (q = 0, u = 0), сила тока в катушке достигнет некоторого значения I m (см. рис. 2, положение 3 ).

Без электрического поля конденсатора (и сопротивления) электроны, создающие ток, продолжают свое движение по инерции. При этом электроны, приходящие на нейтральную обкладку конденсатора, сообщают ей отрицательный заряд, электроны, уходящие с нейтральной обкладки, сообщают ей положительный заряд. На конденсаторе начинает появляться заряд q (и напряжение u ), но противоположного знака, т.е. конденсатор перезаряжается. Теперь новое электрическое поле конденсатора препятствует движению электронов, поэтому сила тока i начинает убывать (см. рис. 2, положение 4 ). Опять же это происходит не мгновенно, поскольку теперь ЭДС самоиндукции стремится скомпенсировать уменьшение тока и «поддерживает» его. А значение силы тока I m (в положении 3 ) оказывается максимальным значением силы тока в контуре.

И снова под действием электрического поля конденсатора в цепи появится электрический ток, но направленный в противоположную сторону, сила тока i которого будет увеличиваться с течением времени. А конденсатор в это время будет разряжаться (см. рис. 2, положение 6 )до нуля (см. рис. 2, положение 7 ). И так далее.

Так как заряд на конденсаторе q (и напряжение u ) определяет его энергию электрического поля W e \(\left(W_{e}=\dfrac{q^{2}}{2C}=\dfrac{C \cdot u^{2}}{2} \right),\) а сила тока в катушке i - энергию магнитного поля Wm \(\left(W_{m}=\dfrac{L \cdot i^{2}}{2} \right),\) то вместе с изменениями заряда, напряжения и силы тока, будут изменяться и энергии.

Обозначения в таблице:

\(W_{e\, \max } =\dfrac{Q_{m}^{2} }{2C} =\dfrac{C\cdot U_{m}^{2} }{2}, \; \; \; W_{e\, 2} =\dfrac{q_{2}^{2} }{2C} =\dfrac{C\cdot u_{2}^{2} }{2}, \; \; \; W_{e\, 4} =\dfrac{q_{4}^{2} }{2C} =\dfrac{C\cdot u_{4}^{2} }{2}, \; \; \; W_{e\, 6} =\dfrac{q_{6}^{2} }{2C} =\dfrac{C\cdot u_{6}^{2} }{2},\)

\(W_{m\; \max } =\dfrac{L\cdot I_{m}^{2} }{2}, \; \; \; W_{m2} =\dfrac{L\cdot i_{2}^{2} }{2}, \; \; \; W_{m4} =\dfrac{L\cdot i_{4}^{2} }{2}, \; \; \; W_{m6} =\dfrac{L\cdot i_{6}^{2} }{2}.\)

Полная энергия идеального колебательного контура сохраняется с течением времени, поскольку в нем потерь энергии (нет сопротивления). Тогда

\(W=W_{e\, \max } = W_{m\, \max } = W_{e2} + W_{m2} = W_{e4} +W_{m4} = ...\)

Таким образом, в идеальном LC -контуре будут происходить периодические изменения значений силы тока i , заряда q и напряжения u , причем полная энергия контура при этом будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания .

• Свободные электромагнитные колебания в контуре - это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.

Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением ЭДС самоиндукции в катушке, которая «обеспечивает» эту перезарядку. Заметим, что заряд конденсатора q и сила тока в катушке i достигают своих максимальных значений Q m и I m в различные моменты времени.

Свободные электромагнитные колебания в контуре происходят по гармоническому закону:

\(q=Q_{m} \cdot \cos \left(\omega \cdot t+\varphi _{1} \right), \; \; \; u=U_{m} \cdot \cos \left(\omega \cdot t+\varphi _{1} \right), \; \; \; i=I_{m} \cdot \cos \left(\omega \cdot t+\varphi _{2} \right).\)

Наименьший промежуток времени, в течение которого LC -контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.

Период свободных электромагнитных колебаний в LC -контуре определяется по формуле Томсона:

\(T=2\pi \cdot \sqrt{L\cdot C}, \;\;\; \omega =\dfrac{1}{\sqrt{L\cdot C}}.\)

Сточки зрения механической аналогии, идеальному колебательному контурусоответствует пружинный маятник без трения, а реальному - с трением. Вследствиедействия сил трения колебания пружинного маятника затухают с течением времени.

*Вывод формулы Томсона

Поскольку полная энергия идеального LC -контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство

\(W=\dfrac{Q_{m}^{2} }{2C} =\dfrac{L\cdot I_{m}^{2} }{2} =\dfrac{q^{2} }{2C} +\dfrac{L\cdot i^{2} }{2} ={\rm const}.\)

Получим уравнение колебаний в LC -контуре, используя закон сохранения энергии. Продифференцировав выражение для его полной энергии по времени, с учетом того, что

\(W"=0, \;\;\; q"=i, \;\;\; i"=q"",\)

получаем уравнение, описывающее свободные колебания в идеальном контуре:

\(\left(\dfrac{q^{2} }{2C} +\dfrac{L\cdot i^{2} }{2} \right)^{{"} } =\dfrac{q}{C} \cdot q"+L\cdot i\cdot i" = \dfrac{q}{C} \cdot q"+L\cdot q"\cdot q""=0,\)

\(\dfrac{q}{C} +L\cdot q""=0,\; \; \; \; q""+\dfrac{1}{L\cdot C} \cdot q=0.\)

Переписав его в виде:

\(q""+\omega ^{2} \cdot q=0,\)

замечаем, что это - уравнение гармонических колебаний с циклической частотой

\(\omega =\dfrac{1}{\sqrt{L\cdot C} }.\)

Соответственно период рассматриваемых колебаний

\(T=\dfrac{2\pi }{\omega } =2\pi \cdot \sqrt{L\cdot C}.\)

Литература

1. Жилко, В.В. Физика: учеб. пособие для 11 класса общеобразоват. шк. с рус. яз. обучения / В.В. Жилко, Л.Г. Маркович. - Минск: Нар. Асвета, 2009. - С. 39-43.