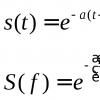И интегрального исчисления к решению физических задач» имеет своей целью изучение курса физики на основе математического анализа.

Данный курс углубляет материал курса алгебры и начал анализа в десятом и одиннадцатом классах и раскрывает возможности для практического закрепления материала по темам, входящим в школьный курс физики. Это темы «Механика», «Электростатика», «Термодинамика» в физике, и некоторые темы алгебре и начал анализа. В результате данный факультативный курс реализует межпредметную связь алгебры и математического анализа с физикой.

Цели факультативного курса.

1. Обучающие: провести практическое закрепление по темам «Механика», «Электростатика», «Термодинамика», проиллюстрировать реализацию межпредметной связи математического анализа с физикой.

2. Воспитывающие: создание условий для успешного профессионального самоопределения учащихся посредством решения трудных задач, воспитание мировоззрения и ряда личностных качеств, средствами углубленного изучения физики.

3. Развивающие: расширение кругозора учащихся, развитие математического мышления, формирование активного познавательного интереса к предмету, развитие профессиональных интересов учащихся, развитие навыков самостоятельной и исследовательской деятельности , развитие рефлексии учащихся (осознание своих склонностей и способностей, необходимыми для будущей профессиональной деятельности).

Примеры решения задач по физике посредствам математического аппарата.

Приложение дифференциального исчисления к решению некоторых задач механики.

1. Работа. Найдем работу, которую совершает заданная сила F при перемещении по отрезку оси х. Если сила F постоянна, то работа А равна произведению F на длину пути. Если сила меняется, то ее можно рассматривать как функцию от х: F = F (x ). Приращение работы А на отрезке [х, x + dx ] нельзя точно вычислить как произведение F (x ) dx , так как сила меняется, на этом отрезке. Однако при маленьких dx можно считать, что сила меняется незначительно и произведение представляет главную часть , т. е. является дифференциалом работы (dA = = F (x ) dx ). Таким образом, силу можно считать производной работы по перемещению.

2. Заряд. Пусть q - заряд, переносимый электрическим током через поперечное сечение проводника за время t . Если сила тока / постоянна, то за время dt ток перенесет заряд, равный Idt . При силе тока, изменяющейся со временем по закону / = /(/), произведение I (t ) dt дает главную часть приращения заряда на маленьком отрезке времени [t , t +- dt ], т.е.- является дифференциалом заряда: dq = I (t ) dt . Следовательно, сила тока является производной заряда по времени.

3. Масса тонкого стержня. Пусть имеется неоднородный тонкий стержень. Если ввести координаты так, как показано на рис. 130, то функция т= т(1) - масса куска стержня от точки О до точки /. Неоднородность стержня означает, что его линейная плотность не является постоянной, а зависит от положения точки / по некоторому закону р = р(/). Если на маленьком отрезке стержня предположить, что плотность постоянна и равна р(/), то произведение p(/)d/ дает дифференциал массы dm . Значит, линейная плотность - это производная массы по длине.

4. Теплота. Рассмотрим процесс нагревания какого-нибудь вещества и вычислим количество теплоты Q { T ), которое необходимо, чтобы нагреть 1 кг вещества от 0 °С до Т. Зависимость Q = Q (T ) очень сложна и определяется экспериментально. Если бы теплоемкость с данного вещества не зависела от температуры, то произведение cdT дало бы изменение количества теплоты. Считая на малом отрезке [T , T + dT ] теплоемкость постоянной, получаем дифференциал количества теплоты dQ = c (T ) dT . Поэтому теплоемкость - это производная теплоты по температуре.

5. Снова работа. Рассмотрим работу как функцию времени. Нам известна характеристика работы, определяющая ее скорость по времени, - это мощность. При работе с постоянной мощностью N работа за время dt равна Ndt . Это выражение представляет дифференциал работы, т.е. dA = N (t ) dt , и мощность выступает как производная работы по времени.

Все приведенные примеры были построены по одному и тому знакомыми нам из курса физики: работа, перемещение, сила; заряд, время, сила тока; масса, длина, линейная плотность; и т. д. Каждый раз одна из этих величин выступала как коэффициент пропорциональности между дифференциалами двумя других, т. е. каждый раз появлялось соотношение вида dy = k (x ) dx . На такое соотношение можно смотреть как на способ определения величины k (x ). Тогда k (x ) находится (или определяется) как производная у по х. Этот вывод мы и фиксировали в каждом примере. Возможна и обратная постановка вопроса: как найти зависимость у от х из заданного соотношения между их дифференциалами.

Приложения определенного интеграла к решению некоторых задач механики.

1.Моменты и центры масс плоских кривых. Если дуга кривой задана уравнением y = f (x ), a ≤ x ≤ b , и имеет плотность = (x ) , то статические моменты этой дуги Mx и My относительно координатных осей Ox и O y равны

https://pandia.ru/text/80/201/images/image004_89.gif" width="215" height="101 src=">а координаты центра масс и - по формулам где l - масса дуги, т. е.

2. Физические задачи. Некоторые применения определенного интеграла при решении физических задач иллюстрируются ниже в примерах.

Скорость прямолинейного движения тела выражается формулой (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.

Так как путь, пройденный телом со скоростью (t ) за отрезок времени , выражается интегралом то имеем:

Уравнение механического движения. Пусть материальная точка массы т движется под действием силы F по оси х. Обозначим t время ее движения, и - скорость, а - ускорение. Второй закон Ньютона, а m = F примет вид дифференциального уравнения, если записать ускорение, а как вторую производную: a = x ’’.

Открытый урок по алгебре и началам анализа в 11 классе с расширенным изучением математики и физики

«Применение методов математического анализа при решении практических задач».

Учитель: Вишневская Н.В.

Цели урока: 1. Повторить основные типы задач, решаемые методами математического анализа.

2. Повторить алгоритмы решения.

3. Разобрать решение задач повышенной трудности.

4. Решить экономические задачи.

План проведения урока:

На доске разбираются две задачи повышенной трудности (карточки № 7 и № 5). Пока ребята готовятся, класс устно отвечает на вопросы:

а) Области, где применяются методы математического анализа;

б) алгоритм решения задач методом поиска наибольших и наименьших значений функции;

в) алгоритм решения задач с помощью определенного интеграла.

В это же время 6 человек работают по карточкам (№ 3, 4, 6, 8, 9, 10).

Заполняются таблицы.

Проверяются задачи на доске, учитель проверяет правильность решения задач по карточкам.

Разбирается на доске экономическая задача (карточка № 1, 2).

Домашняя контрольная работа.

Алгоритм решения задач методом поиска наибольших и наименьших значений функции.

Алгоритм вычисления геометрических и физических величин с помощью определенного интеграла.

Выражают искомую величину как значение в некоторой точке в функции F .

Находят производную f этой функции.

Выражают функцию F в виде определенного интеграла от f и вычисляют его.

Подставляя значение х = b находят искомую величину.

Домашние задачи (на доске):

Карточка № 7

Два корабля движутся по двум перпендикулярным прямым, пересекающимся в точке О , по направлению к О . В какой-то момент времени оба находятся в 65 км от О , скорость первого равна 15 км/ч, второго – 20 км/ч. От первого корабля отходит моторная лодка, движущаяся со скоростью 25 км/ч.

а) За какое наименьшее время катер может доплыть от первого корабля до второго?

б) За какое наименьшее время катер может доплыть от первого корабля до второго и вернуться обратно на первый корабль?

V 1 = 15 км/ч

65 км S 1 О

S 3 S 2

65 км

V л = 25 км/ч

V 2 = 20 км/ч

Решение:

х – время, которое прошло от того момента, когда оба корабля находились в 65 км от О , до момента отправления катера.

– время, которое необходимо катеру на путь от 1-го корабля до 2-го.

В момент отправления катера 1-й корабль был на расстоянии
км от О ; в момент прибытия катера на 2-ой корабль, расстояние между ним и О было равно км; путь катера равен
. Тогда по теореме Пифагора

.

Продифференцируем по х :

;

;

Ответ: а) 1 час; б) 3 часа.

Карточка № 5

Котел имеет форму параболоида вращения. Радиус его основания R = 3 м, глубина Н = 5 м. Котел наполнен жидкостью, удельный вес которой 0,8 Г/см 3 . Вычислить работу, которую нужно произвести, чтобы выкачать жидкость из котла.

у

А R В

dy Н

у

О х х

R = 3 м

Н = 5 м

уд. вес = 0,8 Г/см 3

Вычислить работу, которую нужно произвести, чтобы выкачать жидкость из котла.

Решение:

В плоскости сечения хОу АОВ – парабола, уравнение которой
. Найдем параметр а .

Координаты точки В должны удовлетворять этому уравнению, т.е.

,

, следовательно
.

Разделим параболоид на слои плоскостями, параллельными поверхности жидкости. Пусть толщина слоя на глубине (Н – у) равна dy . Тогда, принимая приближенно слой за цилиндр, получим его объем
.

Из уравнения параболы
, тогда
, т.е. вес слоя жидкости равен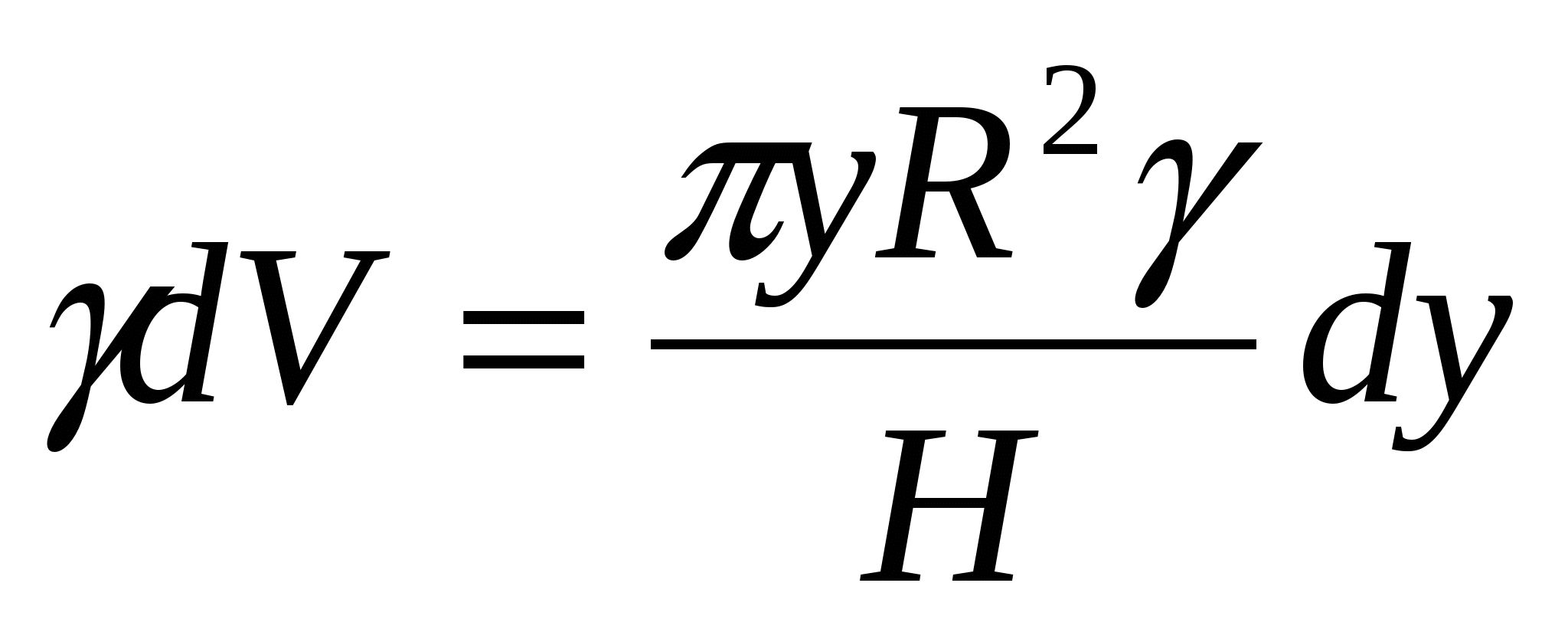
.

Следовательно, чтобы выкачать жидкость с глубины
, потребуется затратить элементарную работу
,
. Тогда

, тогда .

Ответ:
.

Работа в классе.

Карточка № 6

Какую работу нужно затратить, чтобы растянуть пружину на 6 см, если сила 1 кГ растягивает ее на 1 см?

Решение:

Согласно закону Гука сила F кГ, растягивающая пружину на х , равна
, k – коэффициент пропорциональности.

х = 0,01 м

F = 1 кГ

Тогда
, следовательно
.

Искомая работа
.

Ответ: 0,18 кГм.

Карточка № 8

Вычислить работу силы F при сжатии пружины на 5 см, если для сжатия ее на 1 см нужна сила в 1 кг.

Решение:

По закону Гука
.

х = 0,01 м

F = 1 кГ

Тогда
, следовательно
.

Искомая работа
.

Ответ: 0,125 кГм.

Карточка № 9

Сила F , с которой электрический заряд отталкивает заряд (того же знака), находящийся от него на расстоянии r , выражается формулой

,

где k – постоянная.

Определить работу силы F при перемещении заряда из точки , отстоящей от на расстоянии , в точку , отстоящую от на расстоянии , полагая, что заряд помещен в точке , принятой за начало отсчета.

Решение:

Работа определяется по формуле
,
. Тогда

.

При
получим
.

Ответ:
.

Карточка № 3

Определить силу давления воды на вертикальную стенку, имеющую форму полукруга радиуса R = 6 м, диаметр которого находится на поверхности воды.

Решение:

Сила давления жидкости на площадку площадью S при глубине погружения х равна
, – удельный вес жидкости.

О

х С

dх

А В

Полукруг параллельными прямыми разделим на полоски, которые примем за прямоугольник. Пусть заштрихованная полоска имеет длину АВ , ширину dx и находится на глубине х
.

Давление воды на полоску, находящуюся на глубине х , будет равно .

Отсюда

,

,

,

.

Удельный вес воды 1 см 3 = 1 Г, следовательно вес 1м 3 = 1000 кГ.

;

1 кГ 9,81 н

1 бар = 0,987 атм.

Ответ: 144000 кГ.

Карточка № 4

Скорость движения точки
м/сек. Найти путь s , пройденный точкой за время Т = 8 сек после начала движения. Чему равна средняя скорость движения за этот промежуток?

Решение:

, следовательно
,
,
.

Следовательно
.

.

Ответ: 512 м; 64 м/сек.

Карточка № 1 (решается в классе на доске)

Средние совокупные издержки производства мыла (в тыс. рублей на тонну) на Мухинском мыловаренном заводе изменяются в зависимости от объема годового выпуска Q (в тоннах) по закону:

.

Связь между годовым объемом продаж, равным величине годового выпуска Q , и ценой мыла Р (в тыс. рублей за тонну) описывается формулой

.

Реализовав по фиксированной цене все сваренное за год мыло, завод получил максимально возможную прибыль. Какова была при этом выручка предприятия?

Решение:

Выразим через Q сначала цену мыла из формулы
.

.

Тогда прибыль G можно выразить:

Найдем критические точки этой функции:

,
.

Критические точки 100, –340, –120.

Отрицательные корни не имеют экономического смысла.

Q

G

;

.

Значит оптимальный годовой объем мыла
т, тогда цена
(тыс. руб./т).

Тогда годовая выручка R составит: (тыс. руб.).

Ответ: 1 млн. руб.

Карточка № 10

Найти величину давления воды на прямоугольник, вертикально погруженный в воду, если известно, что его основание равно 8 м, высота 12 м, верхнее основание параллельно поверхности воды и находится на глубине 5 м.

Решение:

5 м

8 м

х

dx 12 м

,
,
м.

кГм.

.

Ответ:
кГм.

Карточка № 2 (дополнительная)

Производственные мощности позволяют предприятию «Линотрон» выпускать не более 600 тонн ваты в год. Зависимость величины совокупных издержек (в тыс. рублей) от годового объема производства Q (в тоннах) имеет вид

.

Связь между годовым объемом продаж ваты, который совпадает с объемом годового производства, и ценой на вату Р (в тыс. рублей за тонну) описывается функцией

Цена на вату устанавливается 1 января 1995 года и пересматривается лишь 1 января следующего года.

Найдите с точностью до 1 % рентабельность производства по издержкам, если за 1995 год предприятие получит максимально возможную прибыль.

Решение:

Используя зависимости
и , выразим .

у у

a 0 b c x a 0 b c x

«Омская государственная медицинская академия»

Министерства здравоохранения и социального развития Российской Федерации

на тему: применение определенного интеграла

в медицине

выполнила студент 1 курса

отделения Лечебное дело

группа 102Ф

Глушнева Н.А.

Введение

Выдающийся итальянский физик и астроном, один из основателей точного естествознания, Галилео Галилей (1564-1642) говорил, что "Книга природы написана на языке математики". Почти через двести лет родоначальник немецкой классической философии Кант (1742-1804) утверждал, что "Во всякой науке столько истины, сколько в ней математики". Наконец, ещё через почти сто пятьдесят лет, практически уже в наше время, немецкий математик и логик Давид Гильберт (1862-1943) констатировал: "Математика - основа всего точного естествознания".

Леонардо Да Винчи говорил: «Пусть не читает меня в основах моих тот, кто не математик». Пытаясь найти математическое обоснование законов природы, считая математику могучим средством познания, он применяет ее даже в такой науке, как анатомия.

Математика всем нужна. И медикам тоже. Хотя бы для того, чтобы грамотно прочитать обычную кардиограмму. Без знания азов математики нельзя быть докой в компьютерной технике, использовать возможности компьютерной томографии... Ведь современная медицина не может обходиться без сложнейшей техники.

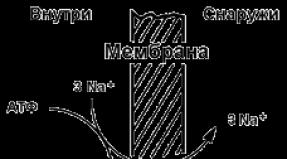
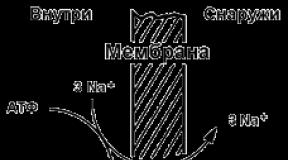
На сегодня невозможно изучение гемодинамики- движения крови по сосудам без применения интеграла.

В течение длительного времени катетеризация правых отделов сердца являлась единственным методом исследования, позволявшим оценивать состояния правых отделов сердца, получать характеристики внутрисердечного кровотока, определять давление в правых отделах сердца и легочной артерии.
Основное преимущество эхокардиографического исследования (ЭхоКГ) заключается в том, что неинвазивно в реальном режиме времени можно оценить размеры и движение сердечных структур, получить характеристики внутрисердечной гемодинамики, определить давление в камерах сердца и легочной артерии. Доказана хорошая сопоставимость результатов ЭхоКГ-исследования с данными, полученными при катетеризации сердца.
ЭхоКГ-исследование позволяет не только выявить наличие легочной гипертензии, но и исключить ряд заболеваний, которые являются причиной вторичной легочной гипертензии: пороки митрального клапана, врожденные пороки сердца, дилатационная кардиомиопатия, хронический миокардит.

Однако, ближе к практике. Для начала найдем линейную скорость кровотока

Изменение линейной скорости кровотока в различных сосудах

Это путь, проходимый в единицу времени частицей крови в сосуде. Линейная скорость в сосудах разного типа различна (см. рисунок) и зависит от объемной скорости кровотока и площади поперечного сечения сосудов. В практической медицине линейную скорость кровотока измеряют с помощью ультразвукового и индикаторного методов, чаще определяют время полного кругооборота крови, которое равно 21-23 с.

Для его определения в локтевую вену вводят индикатор (эритроциты, меченные радиоактивным изотопом, раствор метиленового синего и др.) и отмечают время его первого появления в венозной крови этого же сосуда в другой конечности.

Для начала вспомним, что интеграл- это математический объект, который возник исторически на основе потребности решения различных прикладных задач физики и техники. Это и физические приложения определенного интеграла: вычисление пути материальной точки, движущейся по прямолинейной или криволинейной траектории по скорости ее движения.

Те физические величины, которые определяются с помощью интеграла - как правило, называются интегральными, а те величины, через которые выражаются интегральные величины - дифференциальными. Например, скорость тела в точке - это дифференциальная характеристика тела, а масса тела - интегральная.

Дифференциальные характеристики определяются значением в точке и как правило различны в различных точках пространства.

Интегральные характеристики всегда выражают свойства объектов, относящиеся к целой области пространства. Например, масса характеризует тело целиком как некоторый объект занимающий область пространства. Путь, пройденный телом - это тоже интегральная характеристика, поскольку она характеризует целую траекторию, состоящую из множества точек, а скорость различна в каждой точке траектории и характеризует каждую точку в отдельности.

Возникает вопрос - как же вычислить интегральную скорость для целого сосуда (артерии или вены) , зная линейную скорость кровотока. Очень просто: нужно

• разбить всю область пространства на отдельные достаточно малые части (например взаимно перпендикулярными плоскостями). В этом случае мы получим внутри тела множество мелких кубиков, внутри которых дифференциальную характеристику условно считаем неизменной, постоянной.
• умножить значение дифференциальной характеристики внутри каждого кубика на значение объема этого кубика и просуммировать такие произведения. На этом этапе мы получаем интегральную сумму. Интегральная сумма не равна интегралу в точности, но может служить его приближенным значением.
• перейти к пределу интегральной суммы, когда объем кубиков разбиения тела стремится к нулю. На этом этапе мы получаем точное значение интеграла линейной скорости.

Ниже приведены расчеты ударного объема (ударный объём сердца (син.: систолический объем крови, систолический объем сердца, ударный объем крови) - объем крови (в мл), выбрасываемый желудочком сердца за одну систолу)- одной из основных величин в ЭХОкг, рассчитываемых при помощи интеграла линейной скорости кровотока.

а - Схемы расчета ударного объема, а - с использованием уравнения непрерывности потока, б - с использованием уравнения непрерывности потока при наличии значительной митральной регургитации.

VTI = V cp ЕТ,

где CSA - площадь поперечного сечения, VTI - интеграл линейной скорости потока, V cp - средняя скорость потока в выносящем тракте левого желудочка, ЕТ - время выброса.

В том случае, когда присутствует гемодинамически значимая митральная регургитация (более 2-й степени), тотальный ударный объем левого желудочка рассчитывается по формуле:

TSV = FSV + RSV,

[Интеграл линейной скорости (FVI, или VTI)] = [Время кровотока (ET)] х [Средняя скорость кровотока (Vmean)];

Сердечный выброс может быть определен по интегралу линейной скорости аортального и легочного потока.

В завершении хочу добавить, что моя работа рассчитана не на математика, от и до разбирающегося в интегрировании, а на любого человека, проявившего интерес к применению интеграла в медицине. Поэтому я старалась сделать ее максимально доступной для восприятия и интересной даже ребенку.

Список литературы:

1. Болезни сердца и сосудов http://old.consilium-medicum. com/media/bss/06_02/42.shtml
2. Гемодинамика http://ru.wikipedia.org/wiki/% D0%93%D0%B5%D0%BC%D0%BE%D0%B4% D0%B8%D0%BD%D0%B0%D0%BC%D0%B8% D0%BA%D0%B0
3. Знак интеграла http://ru.wikipedia.org/wiki/% C7%ED%E0%EA_%E8%ED%F2%E5%E3% F0%E0%EB%E0
4. Медицинский консилиум http://www.consilium-medicum. com/article/7144
5. Основные уравнения - Сердце http://serdce.com.ua/osnovnye- uravneniya
6. Практическое руководство по ультразвуковой диагностике http://euromedcompany.ru/ ultrazvuk/prakticheskoe- rukovodstvo-po-ultrazvukovoj- diagnostike

I. В физике

Работа силы

(A=FScos, cos 1)

Если на частицу действует сила F, кинетическая энергия не остается постоянной. В этом случае согласно

приращение кинетической энергии частицы за время dt равно скалярному произведению Fds, где ds - перемещение частицы за время dt. Величина

называется работой, совершаемой силой F.

Пусть точка движется по оси ОХ под действием силы, проекция которой на ось ОХ есть функция f(x) (f-непрерывная функция). Под действием силы точка переместилась из точки S1(a) в S2(b). Разобьем отрезок на n отрезков, одинаковой длины

Работа силы будет равна сумме работ силы на полученных отрезках. Т.к. f(x) -непрерывна, то при малом работа силы на этом отрезке равна

Аналогично на втором отрезке f(x1)(x2-x1), на n-ом отрезке --

f(xn-1)(b-xn-1).

Следовательно работа на равна:

А An = f(a)x +f(x1)x+...+f(xn-1)x= ((b-a)/n)(f(a)+f(x1)+...+f(xn-1))

Приблизительное равенство переходит в точное при n

А = lim [(b-a)/n] (f(a)+...+f(xn-1))= f(x)dx (по определению)

Пусть пружина жесткости С и длины l сжата на половину свой длины. Определить величину потенциальной энергии Ер равна работе A, совершаемой силой -F(s) упругость пружины при её сжатии, то

Eп = A= - (-F(s)) dx

Из курса механики известно, что

Отсюда находим

Еп= - (-Cs)ds = CS2/2 | = C/2 l2/4

Ответ: Cl2/8.

Какую работу надо совершить, чтобы растянуть пружину на 4 см, если известно, что от нагрузки в 1 Н она растягивается на 1 см.

Согласно закону Гука, сила X Н, растягивающая пружину на x, равна

Коэффициент пропорциональности k найдем из условия: если x=0,01 м, то X=1 Н, следовательно, k=1/0,01=100 и X=100x. Тогда

Ответ: A=0,08 Дж

С помощью подъемного крана извлекают железобетонную надолбу со дна реки глубиной 5 м. Какая работа при этом совершится, если надолба имеет форму правильного тетраэдра с ребром 1 м? Плотность железобетона 2500 кг/м3, плотность воды 1000 кг/м3.

Высота тетраэдра

объем тетраэдра

Вес надолбы в воде с учетом действия архимедовой силы равен

Теперь найдем работу Ai при извлечении надолбы из воды. Пусть вершина тетраэдра вышла на высоту 5+y, тогда объем малого тетраэдра, вышедшего из воды, равна, а вес тетраэдра:

Следовательно,

Отсюда A=A0+A1=7227,5 Дж + 2082,5 Дж = 9310 Дж = 9,31 кДж

Ответ: A=9,31 (Дж).

Какую силу давления испытывает прямоугольная пластинка длинной a и шириной b (a>b), если она наклонена к горизонтальной поверхности жидкости под углом б и ее большая сторона находится на глубине h?

Координаты центра масс

Центр масс - точка через которую проходит равнодействующая сил тяжести при любом пространственном расположении тела.

Пусть материальная однородная пластина о имеет форму криволинейной трапеции {x;y |axb; 0yf(x)} и функция

непрерывна на , а площадь этойкриволинейной трапеции равна S, тогда координаты центра масс пластины о находят по формулам:

x0 = (1/S) x f(x) dx; y0 = (1/2S) f 2(x) dx;

Найти центр масс однородного полукруга радиуса R.

Изобразим полукруг в системе координат OXY.

y = (1/2S) (R2-x2)dx = (1/R2) (R2-x2)dx = (1/R2)(R2x-x3/3)|= 4R/3

Ответ: M(0; 4R/3).

Найти координаты центра тяжести фигуры, ограниченной дугой эллипса x=acost, y=bsint, расположенной в I четверти, и осями координат.

В I четверти при возрастании x от 0 до a величина t убывает от р/2 до 0, поэтому

Воспользовавшись формулой площади эллипса S=рab, получим

Путь, пройденный материальной точкой

Если материальная точка движется прямолинейно со скоростью =(t) и за время

T= t2-t1 (t2>t1)

прошла путь S, то

В геометрии

Объём -- количественная характеристика пространственного тела. За единицу измерения объёма принимают куб с ребром 1мм(1дм, 1м и т.д.).

Количество кубов единичного объёма размещенных в данном теле -- объём тела.

Аксиомы объёма:

Объём -- это неотрицательная величина.

Объём тела равен сумме объёмов тел, его составляющих.

Найдем формулу для вычисления объёма:

выберем ось ОХ по направлению расположения этого тела;

определим границы расположения тела относительно ОХ;

введем вспомогательную функцию S(x) задающую следующее соответствие: каждому x из отрезка поставим в соответствие площадь сечения данной фигуры плоскостью, проходящей через заданную точку x перпендикулярно оси ОХ.

разобьем отрезок на n равных частей и через каждую точку разбиения проведём плоскость перпендикулярную оси ОХ, при этом наше тело разобьется на части. По аксиоме

V=V1+V2+...+Vn=lim(S(x1)x +S(x2)x+...+S(xn)x

а объем части, заключенной между двумя соседними плоскостями равна объему цилиндра Vц=SоснH.

Имеем сумму произведений значений функций в точках разбиения на шаг разбиения, т.е. интегральную сумму. По определению определенного интеграла, предел этой суммы при n называется интегралом

где S(x) - сечение плоскости, проходящей через выбранную точку перпендикулярно оси ОХ.

Для нахождения объема надо:

• 1) Выбрать удобным способом ось ОХ.
• 2) Определить границы расположения этого тела относительно оси.
• 3) Построить сечение данного тела плоскостью перпендикулярно оси ОХ и проходящей через соответственную точку.
• 4) Выразить через известные величины функцию, выражающую площадь данного сечения.
• 5) Составить интеграл.
• 6) Вычислив интеграл, найти объем.

Найти объем трехосного эллипса

Плоские сечения эллипсоида, параллельное плоскости xOz и отстоящее от нее на расстоянии y=h, представляет эллипс

Девиз урока: “Математика – язык, на котором говорят все точные науки” Н.И. Лобачевский

Цель урока: обобщить знания учащихся по теме “Интеграл”, “Применение интеграла”;расширить кругозор, знания о возможном применении интеграла к вычислению различных величин; закрепить навыки использовать интеграл для решения прикладных задач; прививать познавательный интерес к математике, развивать культуру общения и культуру математической речи; уметь учиться выступать перед учащимися и учителями.

Тип урока: повторительно-обобщающий.

Вид урока: урок – защита проекта “Применение интеграла”.

Оборудование: магнитная доска, плакаты “Применение интеграла”, карточки с формулами и заданиями для самостоятельной работы.

План урока:

1. Защита проекта:

1. из истории интегрального исчисления;
2. свойства интеграла;
3. применение интеграла в математике;
4. применение интеграла в физике;

2. Решение упражнений.

Ход урока

Учитель: Мощным средством исследования в математике, физике, механике и других дисциплинах является определенный интеграл – одно из основных понятий математического анализа. Геометрический смысл интеграла – площадь криволинейной трапеции. Физический смысл интеграла – 1) масса неоднородного стержня с плотностью, 2) перемещение точки, движущейся по прямой со скоростью за промежуток времени.

Учитель: Ребята нашего класса провели большую работу, они подобрали задачи, где применяется определенный интеграл. Им слово.

2 ученик: Свойства интеграла

3 ученик: Применение интеграла (на магнитной доске таблица).

4 ученик: Рассматриваем применение интеграла в математике для вычисления площади фигур.

Площадь всякой плоской фигуры, рассматриваемая в прямоугольной системе координат, может быть составлена из площадей криволинейных трапеций, прилежащих к оси Ох и оси Оу. Площадь криволинейной трапеции, ограниченной кривой у = f(х), осью Ох и двумя прямыми х=а и х=b, где а х b , f(х) 0 вычисляется по формуле см. рис. Если криволинейная трапеция прилегает к оси Оу , то её площадь вычисляется по формуле , см. рис. При вычислении площадей фигур могут представиться следующие случаи: а)Фигура расположена над осью Ох и ограничена осью Ох, кривой у=f(х) и двумя прямыми х=а и х=b.(См. рис. ) Площадь этой фигуры находится по формуле 1 или 2. б) Фигура расположена под осью Ох и ограничена осью Ох, кривой у=f(х) и двумя прямыми х=а и х=b (см. рис. ). Площадь находится по формуле . в) Фигура расположена над и под осью Ох и ограничена осью Ох, кривой у=f(х) и двумя прямыми х=а и х=b(рис. ). г) Площадь ограничена двумя пересекающимися кривыми у=f(х) и у = (х) (рис. )

5 ученик: Решим задачу

х-2у+4=0 и х+у-5+0 и у=0

7 ученик: Интеграл, широко применяющийся в физике. Слово физикам.

1. ВЫЧИСЛЕНИЕ ПУТИ, ПРОЙДЕННОГО ТОЧКОЙ

Путь, пройденный точкой при неравномерном движении по прямой с переменной скоростью за промежуток времени от до вычисляется по формуле .

Примеры:

1. Скорость движения точки м/с. Найти путь, пройденный точкой за 4-ю секунду.

Решение: согласно условию, . Следовательно,

2. Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью м/с, второе - со скоростью v = (4t+5) м/с. На каком расстоянии друг от друга они окажутся через 5 с?

Решение: очевидно, что искомая величина есть разность расстояний, пройденных первым и вторым телом за 5 с:

3. Тело брошено с поверхности земли вертикально вверх со скоростью и = (39,2-9,8^) м/с. Найти наибольшую высоту подъема тела.

Решение: тело достигнет наибольшей высоты подъема в такой момент времени t, когда v = 0, т.е. 39,2-9,8t = 0, откуда I = 4 с. По формуле (1) на ходим

2. ВЫЧИСЛЕНИЕ РАБОТЫ СИЛЫ

Работа, произведенная переменной силой f(х) при перемещении по оси Ох материальной точки от х = а до х=b, находится по формуле При решении задач на вычисление работы силы часто используется закон Г у к а: F=kx, (3) где F - сила Н; х -абсолютное удлинение пружины, м, вызванное силой F , а k -коэффициент пропорциональности, Н/м.

Пример:

1. Пружина в спокойном состоянии имеет длину 0,2 м. Сила в 50 Н растягивает пружину на 0,01 м. Какую работу надо совершить, чтобы растянуть ее от 0,22 до 0,32 м?

Решение: используя равенство (3), имеем 50=0,01k, т. е. kК = 5000 Н/м. Находим пределы интегрирования: а = 0,22 - 0,2 = 0,02 (м), b=0,32 - 0,2 = 0,12(м). Теперь по формуле (2) получим

3. ВЫЧИСЛЕНИЕ РАБОТЫ, ПРОИЗВОДИМОЙ ПРИ ПОДНЯТИИ ГРУЗА

Задача. Цилиндрическая цистерна с радиусом основания 0,5 м и высотой 2 м заполнена водой. Вычислить работу, которую необходимо произвести, чтобы выкачать воду из цистерны.

Решение: выделим на глубине х горизонтальный слой высотой dх (рис. ). Работа А, которую надо произвести, чтобы поднять слой воды весом Р на высоту х, равна Рх.

Изменение глубины х на малую величину dх вызовет изменение объема V на величину dV = пr 2 dх и изменение веса Р на величину * dР = 9807 r 2 dх; при этом совершаемая работа А изменится на величину dА=9807пr 2 хdх. Проинтегрировав это равенство при изменении x от 0 до Н, получим

4. ВЫЧИСЛЕНИЕ СИЛЫ ДАВЛЕНИЯ ЖИДКОСТИ

Значение силы Р давления жидкости на горизонтальную площадку зависит от глубины погружения х этой площадки, т. е. от расстояния площадки до поверхности жидкости.

Сила давления (Н) на горизонтальную площадку вычисляется по формуле Р =9807 S x,

где - плотность жидкости, кг/м 3 ; S - площадь площадки, м 2 ; х - глубина погружения площадки, м.

Если площадка, испытывающая давление жидкости, не горизонтальна, то давление на нее различно на разных глубинах, следовательно, сила давления на площадку есть функция глубины ее погружения Р (х).

5. ДЛИНА ДУГИ

Пусть плоская кривая АВ (рис.) задана уравнением у =f(x) (a x b), причем f(x) и f ?(x) - непрерывные функции в промежутке [а,b]. Тогда дифференциал dl длины дуги АВ выражается формулой или , а длина дуги АВ вычисляется по формуле (4)

где а и b-значения независимой переменной х в точках А и В. Если кривая задана уравнением х = (у)(с у d), то длина дуги АВ вычисляется по формуле (5) где с и д значения независимой переменной у в точках А и В.

6. ЦЕНТР МАСС

При нахождении центра масс пользуются следующими правилами:

1) Координата х? центра масс системы материальных точек А 1 , А 2 ,..., А n с массами m 1 , m 2 , ..., m n , расположенных на прямой в точках с координатами х 1 , х 2 , ..., х n , находятся по формуле

(*); 2) При вычислении координаты центра масс можно любую часть фигуры заменить на материальную точку, поместив ее в центр масс этой части, и приписать ей массу, равную массе рассматриваемой части фигуры. Пример. Пусть вдоль стержня-отрезка [а;b] оси Ох - распределена масса плотностью (х), где (х) - непрерывная функция. Покажем, что а) суммарная масса М стержня равна ; б) координата центра масс х" равна .

Разобьем отрезок [а; b] на n равных частей точками а= х 0 < х 1 < х 2 < ... <х n = b (рис. ). На каждом из n этих отрезков плотность можно считать при больших n постоянно и примерно равной (х k - 1) на k-м отрезке (в силу непрерывности (х). Тогда масса k-ого отрезка примерно равна а масса всего стержня равна

Считая каждый из n маленьких отрезков материальной точкой массы m k , помещенной в точке , получим по формуле (*), что координата центра масс приближенно находится так

Теперь осталось заметить, что при n -> числитель стремится к интегралу , а знаменатель (выражающий массу всего стержня) - к интегралу

Для нахождения координат центра масс системы материальных точек на плоскости или в пространстве также пользуются формулой(*)

Учитель: У вас на столах таблица и задачи, используя таблицу найдите: а) количество электричества; б) массу стержня по его плотности.

Величины

Вычисление производной

Вычисление интеграла Вариант 1 Вариант 2 Итог урока: Завершили тему “Интеграл”, научились вычислять первообразные, интегралы, площади фигур, рассмотрели применение интеграла на практике, данные задачи могут встретиться на ЕГЭ, думаю, с ними вы справитесь.