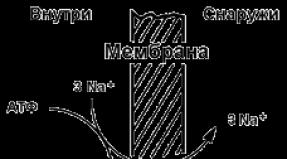
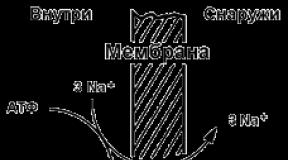
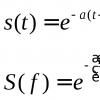Презентация неопределенный интеграл функции спо. Первообразная и интеграл. Основные свойства определенного интеграла
03.05.2020 Удивительное
Cлайд 1
Cлайд 2
 Исторические сведения Интегральное исчисление возникло из потребности создать общий метод Разыскания площадей, объемов и центров тяжести. В зародышевой форме такой метод применялся ещё Архимедом. Систе- Матическое развитие он получил в 17-м веке в работах Кавальери,Торриче- лли, Фермам,Паскаля. В 1659 г. И.Барроу установил связь мемжду задачей о разыскании площади и задачей о разыскании касательной. Ньютон и Лейб- Ниц в 70-х годах 17-го века отвлекли эту связь от упомянутых частных геомет- Рических задач. Тем мсамым была установлена связь между интегральным и Дифференциальным исчислением. Эта связь была использована Ньютоном, Лейбницем и их учениками для Развития техники интегрирования. Своего нынешнего состояния методы интег- Рирования в основном достигли в работах Л.Эйлера. Труды М.В.Остроградско- Го и П.Л.Чебышева завершили развитие этих методов.
Исторические сведения Интегральное исчисление возникло из потребности создать общий метод Разыскания площадей, объемов и центров тяжести. В зародышевой форме такой метод применялся ещё Архимедом. Систе- Матическое развитие он получил в 17-м веке в работах Кавальери,Торриче- лли, Фермам,Паскаля. В 1659 г. И.Барроу установил связь мемжду задачей о разыскании площади и задачей о разыскании касательной. Ньютон и Лейб- Ниц в 70-х годах 17-го века отвлекли эту связь от упомянутых частных геомет- Рических задач. Тем мсамым была установлена связь между интегральным и Дифференциальным исчислением. Эта связь была использована Ньютоном, Лейбницем и их учениками для Развития техники интегрирования. Своего нынешнего состояния методы интег- Рирования в основном достигли в работах Л.Эйлера. Труды М.В.Остроградско- Го и П.Л.Чебышева завершили развитие этих методов.
Cлайд 3
 Понятие об интеграле. Пусть линия MN дана уравнением И надо найти площадь F «криволинейной трапеции aABb. Разделим отрезок ab на n частей (равных или неравных) и построим ступенчатую фигуру, показанную штриховкой на черт.1 Её площадь, её площадь равна (1) Если ввести обозначения То формула (1) примет вид (3) Искомая площадь есть предел суммы (3) при бесконечно большом n. Лейбниц ввёл для этого предела обозначение (4) В котором (курсивное s) – начальная буква слова summa (сумма), Е выражение указывает типичную форму отдельных слагае- Мых. Выражение Лейбниц стал называть интегралом – от латинско- Го слова integralis – целостный. Ж.Б.Фурье усовершенствовал обоз- Начение Лейбница, придав ему вид Здесь явно указаны начальное и конечное значе- ния x .
Понятие об интеграле. Пусть линия MN дана уравнением И надо найти площадь F «криволинейной трапеции aABb. Разделим отрезок ab на n частей (равных или неравных) и построим ступенчатую фигуру, показанную штриховкой на черт.1 Её площадь, её площадь равна (1) Если ввести обозначения То формула (1) примет вид (3) Искомая площадь есть предел суммы (3) при бесконечно большом n. Лейбниц ввёл для этого предела обозначение (4) В котором (курсивное s) – начальная буква слова summa (сумма), Е выражение указывает типичную форму отдельных слагае- Мых. Выражение Лейбниц стал называть интегралом – от латинско- Го слова integralis – целостный. Ж.Б.Фурье усовершенствовал обоз- Начение Лейбница, придав ему вид Здесь явно указаны начальное и конечное значе- ния x .
Cлайд 4
 Связь между интегрированием и дифференцированием. Будем считать а постоянной, а b – переменной величиной. Тогда интеграл будет функцией от b . Дифференциал этой функции равен
Связь между интегрированием и дифференцированием. Будем считать а постоянной, а b – переменной величиной. Тогда интеграл будет функцией от b . Дифференциал этой функции равен
Cлайд 5
 Первообразная функция. Пусть функция есть производная от функции, Т.С. Есть дифференциал функции: Тогда функция называется первообразной для функции
Первообразная функция. Пусть функция есть производная от функции, Т.С. Есть дифференциал функции: Тогда функция называется первообразной для функции
Cлайд 6
 Пример нахождения первообразной. Функция есть первообразная от Т.С. Есть дифференциал функции Функция является первообразной для функции
Пример нахождения первообразной. Функция есть первообразная от Т.С. Есть дифференциал функции Функция является первообразной для функции
Cлайд 7
 Неопределённый интеграл. Неопределённым интегралом данного выражения Называется наиболее общий вид его первообразной функции. Неопределённый интеграл выражения обозначается Выражение называется подинтегральным выражением, Функция -подинтегральной функцией, переменная x –перемен- Ной интегрирования. Разыскание неопределённого интеграла данной Функции называется интегрированием.
Аношина О.В.
Неопределённый интеграл. Неопределённым интегралом данного выражения Называется наиболее общий вид его первообразной функции. Неопределённый интеграл выражения обозначается Выражение называется подинтегральным выражением, Функция -подинтегральной функцией, переменная x –перемен- Ной интегрирования. Разыскание неопределённого интеграла данной Функции называется интегрированием.
Аношина О.В.Основная литература
1. Шипачев В. С. Высшая математика. Базовый курс: учебник ипрактикум для бакалавров [Гриф Минобразования РФ] / В. С.
Шипачев; под ред. А. Н. Тихонова. - 8-е изд., перераб. и доп. Москва: Юрайт, 2015. - 447 с.
2. Шипачев В. С. Высшая математика. Полный курс: учебник
для акад. бакалавриата [Гриф УМО] / В. С. Шипачев; под ред. А.
Н. Тихонова. - 4-е изд., испр. и доп. - Москва: Юрайт, 2015. - 608
с
3. Данко П.Е., Попов А.Г., Кожевникова Т..Я. Высшая математика
в упражнениях и задачах. [Текст] / П.Е. Данко, А.Г. Попов, Т.Я.
Кожевникова. В 2 ч. – М.: Высшая школа, 2007. – 304+415c.
Отчетность
1.Контрольная работа. Выполняется в соответствии:
Задания и методические указания к выполнению контрольных работ
по дисциплине «ПРИКЛАДНАЯ МАТЕМАТИКА», Екатеринбург, ФГАОУ
ВО «Российский государственный профессионально-педагогический
университет», 2016 - 30с.
Вариант контрольной работы выбирать по последней цифре номера
зачетной книжки.
2.
Экзамен
Неопределенный интеграл, его свойства и вычисление Первообразная и неопределенный интеграл
Определение. Функция F x называетсяпервообразной функции f x , определенной на
некотором промежутке, если F x f x для
каждого x из этого промежутка.
Например, функция cos x является
первообразной функции sin x , так как
cos x sin x .Очевидно, если F x - первообразная
функции f x , то F x C , где C некоторая постоянная, также является
первообразной функции f x .
Если F x есть какая-либо первообразная
функции f x , то всякая функция вида
Ф x F x C также является
первообразной функции f x и всякая
первообразная представима в таком виде.Определение. Совокупность всех
первообразных функции f x ,
определенных на некотором
промежутке, называется
неопределенным интегралом от
функции f x на этом промежутке и
обозначается f x dx .Если F x - некоторая первообразная функции
f x , то пишут f x dx F x C , хотя
правильнее бы писать f x dx F x C .
Мы по устоявшейся традиции будем писать
f x dx F x C .
Тем самым один и тот же символ
f x dx будет обозначать как всю
совокупность первообразных функции f x ,
так и любой элемент этого множества.
Свойства интеграла
Производная неопределенного интеграла равнаподынтегральной функции, а его дифференциалподынтегральному выражению. Действительно:
1.(f (x)dx) (F (x) C) F (x) f (x);
2.d f (x)dx (f (x)dx) dx f (x)dx.
Свойства интеграла
3. Неопределенный интеграл отдифференциала непрерывно (x)
дифференцируемой функции равен самой
этой функции с точностью до постоянной:
d (x) (x)dx (x) C,
так как (x) является первообразной для (x).
Свойства интеграла
4.Если функции f1 x и f 2 x имеютпервообразные, то функция f1 x f 2 x
также имеет первообразную, причем
f1 x f 2 x dx f1 x dx f 2 x dx ;
5. Kf x dx K f x dx ;
6. f x dx f x C ;
7. f x x dx F x C .
1. dx x C .
a 1
x
2. x a dx
C, (a 1) .
a 1
dx
3. ln x C .
x
x
a
4. a x dx
C .
ln a
5. e x dx e x C .
6. sin xdx cos x C .
7. cos xdx sin x C .
dx
8. 2 ctgx C .
sin x
dx
9. 2 tgx C .
cos x
dx
arctgx C .
10.
2
1 x
Таблица неопределенных интегралов
11.dx
arcsin x C .
1 x 2
dx
1
x
12. 2 2 arctg C .
a
a
a x
13.
14.
15.
dx
a2 x2
x
arcsin C ..
a
dx
1
x a
ln
C
2
2
2a x a
x a
dx
1
a x
a 2 x 2 2a ln a x C .
dx
16.
x2 a
ln x x 2 a C .
17. shxdx chx C .
18. chxdx shx C .
19.
20.
dx
ch 2 x thx C .
dx
cthx C .
2
sh x
Свойства дифференциалов
При интегрировании удобно пользоватьсясвойствами: 1
1. dx d (ax)
a
1
2. dx d (ax b),
a
1 2
3. xdx dx ,
2
1 3
2
4. x dx dx .
3
Примеры
Пример. Вычислить cos 5xdx .Решение. В таблице интегралов найдем
cos xdx sin x C .
Преобразуем данный интеграл к табличному,
воспользовавшись тем, что d ax adx .
Тогда:
d 5 x 1
= cos 5 xd 5 x =
cos 5xdx cos 5 x
5
5
1
= sin 5 x C .
5
Примеры
Пример. Вычислить x3x x 1 dx .
Решение. Так как под знаком интеграла
находится сумма четырех слагаемых, то
раскладываем интеграл на сумму четырех
интегралов:
2
3
2
3
2
3
x
3
x
x
1
dx
x
dx
3
x
dx xdx dx .
x3
x4 x2
3
x C
3
4
2
Независимость от вида переменной
При вычислении интегралов удобнопользоваться следующими свойствами
интегралов:
Если f x dx F x C , то
f x b dx F x b C .
Если f x dx F x C , то
1
f ax b dx F ax b C .
a
Пример
Вычислим1
6
2
3
x
dx
2
3
x
C
.
3 6
5
Методы интегрирования Интегрирование по частям
Этот метод основан на формуле udv uv vdu .Методом интегрирования по частям берут такие интегралы:
а) x n sin xdx , где n 1,2...k ;
б) x n e x dx , где n 1,2...k ;
в) x n arctgxdx , где n 0, 1, 2,... k . ;
г) x n ln xdx , где n 0, 1, 2,... k .
При вычислении интегралов а) и б) вводят
n 1
обозначения: x n u , тогда du nx dx , а, например
sin xdx dv ,тогда v cos x .
При вычислении интегралов в), г) обозначают за u функцию
arctgx , ln x , а за dv берут x n dx .
Примеры
Пример. Вычислить x cos xdx .Решение.
u x, du dx
=
x cos xdx
dv cos xdx, v sin x
x sin x sin xdx x sin x cos x C .
Примеры
Пример. Вычислитьx ln xdx
dx
u ln x, du
x
x2
dv xdx, v
2
x2
x 2 dx
ln x
=
2
2 x
x2
1
x2
1 x2
ln x xdx
ln x
C .
=
2
2
2
2 2
Метод замены переменной
Пусть требуется найти f x dx , причемнепосредственно подобрать первообразную
для f x мы не можем, но нам известно, что
она существует. Часто удается найти
первообразную, введя новую переменную,
по формуле
f x dx f t t dt , где x t , а t - новая
переменная
Интегрирование функций, содержащих квадратный трехчлен
Рассмотрим интегралax b
dx ,
x px q
содержащий квадратный трехчлен в
знаменателе подынтегрального
выражения. Такой интеграл берут также
методом замены переменных,
предварительно выделив в
знаменателе полный квадрат.
2
Пример
Вычислитьdx
.
x 4x 5
Решение. Преобразуем x 2 4 x 5 ,
2
выделяя полный квадрат по формуле a b 2 a 2 2ab b 2 .
Тогда получаем:
x2 4x 5 x2 2 x 2 4 4 5
x 2 2 2 x 4 1 x 2 2 1
x 2 t
dx
dx
dt
x t 2
2
2
2
x 2 1 dx dt
x 4x 5
t 1
arctgt C arctg x 2 C.
Пример
Найти1 x
1 x
2
dx
tdt
1 t
2
x t, x t 2 ,
dx 2tdt
2
t2
1 t
2
dt
1 t
1 t
d (t 2 1)
t
2
1
2
2tdt
2
dt
ln(t 1) 2 dt 2
2
1 t
ln(t 2 1) 2t 2arctgt C
2
ln(x 1) 2 x 2arctg x C.
1 t 2 1
1 t
2
dt
Определенный интеграл, его основные свойства. Формула Ньютона- Лейбница. Приложения определенного интеграла.
К понятию определенного интеграла приводитзадача нахождения площади криволинейной
трапеции.
Пусть на некотором интервале задана
непрерывная функция y f (x) 0
Задача:
Построить ее график и найти F площадь фигуры,
ограниченной этой кривой, двумя прямыми x = a и x
= b, а снизу – отрезком оси абсцисс между точками
x = a и x = b.Фигура aABb называется
криволинейной трапецией
Определение
bf (x)dx
Под определенным интегралом
a
от данной непрерывной функции f(x) на
данном отрезке понимается
соответствующее приращение ее
первообразной, то есть
F (b) F (a) F (x) /
b
a
Числа a и b – пределы интегрирования,
– промежуток интегрирования.
Правило:
Определенный интеграл равен разностизначений первообразной подынтегральной
функции для верхнего и нижнего пределов
интегрирования.
Введя обозначения для разности
b
F (b) F (a) F (x) / a
b
f (x)dx F (b) F (a)
a
Формула Ньютона – Лейбница.
Основные свойства определенного интеграла.
1)Величина определенного интеграла не зависит отобозначения переменной интегрирования, т.е.
b
b
a
a
f (x)dx f (t)dt
где x и t – любые буквы.
2)Определенный интеграл с одинаковыми
пределами
интегрирования равен нулю
a
f (x)dx F (a) F (a) 0
a3) При перестановке пределов интегрирования
определенный интеграл меняет свой знак на обратный
b
a
f (x)dx F (b) F (a) F (a) F (b) f (x)dx
a
b
(свойство аддитивности)
4) Если промежуток разбит на конечное число
частичных промежутков, то определенный интеграл,
взятый по промежутку , равен сумме определенных
интегралов, взятых по всем его частичным промежуткам.
b
c
b
f (x)dx f (x)dx
c
a
a
f (x)dx5)Постоянный множитель можно выносить
за знак определенного интеграла.
6)Определенный интеграл от алгебраической
суммы конечного числа непрерывных
функций равен такой же алгебраической
сумме определенных интегралов от этих
функций.
3. Замена переменной в определенном интеграле.
3. Замена переменной в определенноминтеграле.
b
f (x)dx f (t) (t)dt
a
a (), b (), (t)
где
для t [ ; ] , функции (t) и (t) непрерывны на;
5
Пример:
1
=
x 1dx
=
x 1 5
t 0 4
x 1 t
dt dx
4
0
3
2
t dt t 2
3
4
0
2
2
16
1
t t 40 4 2 0
5
3
3
3
3
Несобственные интегралы.
Несобственные интегралы.Определение. Пусть функция f(x) определена на
бесконечном интервале , где b < + . Если
существует
b
lim
f (x)dx,
b
a
то этот предел называется несобственным
интегралом функции f(x) на интервале
}