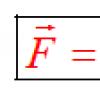Təcrübədə çox vaxt triqonometrik funksiyaları ehtiva edən transsendental funksiyaların inteqrallarını hesablamaq lazımdır. Bu materialın bir hissəsi olaraq biz inteqral funksiyaların əsas növlərini təsvir edəcəyik və onları inteqrasiya etmək üçün hansı üsullardan istifadə edilə biləcəyini göstərəcəyik.

Sinus, kosinus, tangens və kotangensin inteqrasiyası

Əsas triqonometrik funksiyaların - sin, cos, t g, c t g inteqrasiyası üsullarından başlayaq. Antitörəmələr cədvəlindən istifadə edərək dərhal yazırıq ki, ∫ sin x d x = - cos x + C, və ∫ cos x d x = sin x + C.

t g və c t g funksiyalarının qeyri-müəyyən inteqrallarını hesablamaq üçün diferensial işarədən istifadə edə bilərsiniz:

∫ t g x d x = ∫ sin x cos x d x = d (cos x) = - sin x d x = = - ∫ d (cos x) cos x = - ln cos x + C ∫ c t g x d x = ∫ cos x sin x d x = d (sin x) = cos x d x = = ∫ d (sin x) sin x = ln sin x + C

Antiderivativlər cədvəlindən götürülmüş ∫ d x sin x = ln 1 - cos x sin x + C və ∫ d x cos x = ln 1 + sin x cos x + C düsturlarını necə əldə etdik? Yalnız bir halı izah edək, çünki ikincisi bənzətmə ilə aydın olacaq.

Əvəzetmə metodundan istifadə edərək yazırıq:

∫ d x sin x = sin x = t ⇒ x = a r c sin y ⇒ d x = d t 1 - t 2 = d t t 1 - t 2

Burada irrasional funksiyanı inteqrasiya etməliyik. Eyni əvəzetmə metodundan istifadə edirik:

∫ d t t 1 - t 2 = 1 - t 2 = z 2 ⇒ t = 1 - z 2 ⇒ d t = - z d z 1 - z 2 = = ∫ - z d z z 1 - z 2 1 - z 2 = ∫ - z ∫ d z (z - 1) (z +) = = 1 2 ∫ d z z - 1 - 1 2 ∫ d z z + 1 = 1 2 ln z - 1 - 1 2 z + 1 + C = = 1 2 ln z - 1 z + 1 + C = ln z - 1 z + 1 + C

İndi z = 1 - t 2 və t = sin x əvəzedicisini yerinə yetiririk:

∫ d x sin x = ∫ d t t 1 - t 2 = ln z - 1 z + 1 + C = = ln 1 - t 2 - 1 1 - t 2 + 1 + C = ln 1 - sin 2 x - 1 1 - sin 2 x + 1 + C = = ln cos x - 1 cos x + 1 + C = ln (cos x - 1) 2 sin 2 x + C = = ln cos x - 1 sin x + C

∫ sin n x d x, ∫ cos n x d x, ∫ d x sin n x, ∫ d x cos n x kimi triqonometrik funksiyaların səlahiyyətlərini ehtiva edən inteqrallı halları ayrıca təhlil edəcəyik.

Onları necə düzgün hesablamaq barədə təkrar düsturlardan istifadə edərək inteqrasiya haqqında məqalədə oxuya bilərsiniz. Bu düsturların necə alındığını bilirsinizsə, təbii m və n ilə ∫ sin n x · cos m x d x kimi inteqralları asanlıqla qəbul edə bilərsiniz.

Əgər triqonometrik funksiyaların çoxhədli və ya eksponensial funksiyalarla kombinasiyası varsa, onda onlar hissələrlə inteqral edilməli olacaqlar. ∫ P n (x) · sin (a x) d x , ∫ P n (x) · cos (a x) d x , ∫ e a · x · sin (a x) d x , ∫ e a inteqrallarının tapılması üsullarına həsr olunmuş məqaləni oxumağı tövsiyə edirik. · x · cos (a x) d x .

Ən çətin məsələlər inteqralın müxtəlif arqumentləri olan triqonometrik funksiyaları ehtiva etdiyi məsələlərdir. Bunu etmək üçün əsas triqonometriya düsturlarından istifadə etməlisiniz, ona görə də onları əzbərləmək və ya əlinizdə qeyd saxlamaq məsləhətdir.

Misal 1

y = sin (4 x) + 2 cos 2 (2 x) sin x · cos (3 x) + 2 cos 2 x 2 - 1 · sin (3 x) funksiyasının əks törəmələri çoxluğunu tapın.

Həll

Dərəcəni azaltmaq üçün düsturlardan istifadə edək və yazaq ki, cos 2 x 2 = 1 + cos x 2, cos 2 2 x = 1 + cos 4 x 2. O deməkdir ki,

y = sin (4 x) + 2 cos 2 (2 x) sin x cos (3 x) + 2 cos 2 x 2 - 1 sin (3 x) = sin (4 x) + 2 1 + cos 4 x 2 sin x cos (3 x) + 2 1 + cos x 2 - 1 sin (3 x) = = sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x)

Məxrəcdə cəminin sinusunun düsturu var. Sonra bunu belə yaza bilərsiniz:

y = sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x) = sin (4 x) + cos (4 x) + 1 sin (4 x ) = = 1 + cos (4 x) sin (4 x)

3 inteqralın cəmini aldıq.

∫ sin (4 x) + cos (4 x) + 1 sin x · cos (3 x) + cos x · sin (3 x) d x = = ∫ d x + cos (4 x) d x sin (4 x) + ∫ d x sin (4 x) = = x + 1 4 ln ∫ d (sin (4 x)) sin (4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) = = 1 4 ln sin ( 4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) + C = x + 1 4 ln cos 4 x - 1 + C

Bəzi hallarda inteqralın altındakı triqonometrik funksiyalar standart əvəzetmə metodundan istifadə etməklə kəsrli rasional ifadələrə endirilə bilər. Əvvəlcə sin, cos və t g-ni yarım arqumentin tangensi ilə ifadə edən düsturları götürək:

sin x = 2 t g x 2 1 + t g 2 x 2 , sin x = 1 - t g 2 x 2 1 + t g 2 x 2 , t g x = 2 t g x 2 1 - t g 2 x 2

Biz həmçinin d x diferensialını yarım bucağın tangensi ilə ifadə etməliyik:

d t g x 2 = t g x 2 "d x = d x 2 cos 2 x 2 olduğundan

d x = 2 cos 2 x 2 d t g x 2 = 2 d t g x 2 1 cos 2 x 2 = 2 d t g x 2 cos 2 x 2 + sin 2 x 2 cos 2 x 2 = 2 d t g x 2 1 + t g 2 x 2

Beləliklə, sin x = 2 z 1 + z 2, cos x 1 - z 2 1 + z 2, t g x 2 z 1 - z 2, d x = 2 d z 1 + z 2 at z = t g x 2.

Misal 2

∫ d x 2 sin x + cos x + 2 qeyri-müəyyən inteqralını tapın.

Həll

Standart triqonometrik əvəzetmə metodundan istifadə edirik.

2 sin x + cos x + 2 = 2 2 z 1 + z 2 + 1 - z 2 1 + z 2 = z 2 + 4 z + 3 1 + z 2 ⇒ d x 2 sin x + cos x + 2 = 2 d z 1 + z 2 z 2 + 4 z + 3 1 + z 2 = 2 d z z 2 + 4 z + 3

Alırıq ki, ∫ d x 2 sin x + cos x + 2 = 2 d z z 2 + 4 z + 3 .

İndi inteqranı sadə kəsrlərə genişləndirə və iki inteqralın cəmini əldə edə bilərik:

∫ d x 2 sin x + cos x + 2 = 2 ∫ 2 d z z 2 + 4 z + 3 = 2 ∫ 1 2 1 z + 1 - 1 z + 3 d z = = ∫ d z z + 1 - ∫ C z + 3 = l z + 1 - ln z + 3 + C = ln z + 1 z + 3 + C

∫ d x 2 sin x + cos x + 2 = ln z + 1 z + 3 + C = ln t g x 2 + 1 t g x 2 + 3 + C

Cavab: ∫ d x 2 sin x + cos x + 2 = ln t g x 2 + 1 t g x 2 + 3 + C

Qeyd etmək lazımdır ki, funksiyaları yarım arqumentin tangensi ilə ifadə edən düsturlar eynilik deyil, buna görə də nəticədə ln t g x 2 + 1 t g x 2 + 3 + C ifadəsi y = 1 2 funksiyasının əks törəmələri çoxluğudur. sin x + cos x + 2 yalnız tərif sahəsində.

Digər növ problemləri həll etmək üçün əsas inteqrasiya üsullarından istifadə edə bilərsiniz.

Mətndə xəta görsəniz, onu vurğulayın və Ctrl+Enter düymələrini basın

Triqonometrik funksiyaların inteqralları.
Həll nümunələri

Bu dərsdə triqonometrik funksiyaların inteqrallarına baxacağıq, yəni inteqralların doldurulması müxtəlif kombinasiyalarda sinuslar, kosinuslar, tangenslər və kotangentlər olacaqdır. Bütün nümunələr ətraflı təhlil ediləcək, hətta bir çaynik üçün də əlçatan və başa düşüləcək.

Triqonometrik funksiyaların inteqrallarını uğurla öyrənmək üçün siz ən sadə inteqralları yaxşı başa düşməlisiniz, həmçinin bəzi inteqrasiya üsullarını mənimsəməlisiniz. Bu materiallarla mühazirələrdə tanış ola bilərsiniz Qeyri-müəyyən inteqral. Həll nümunələri Və .

İndi bizə lazımdır: İnteqrallar cədvəli, Törəmələr cədvəli Və Triqonometrik düsturlar kataloqu. Bütün tədris vəsaitlərini səhifədə tapa bilərsiniz Riyazi düsturlar və cədvəllər. Hər şeyi çap etməyi məsləhət görürəm. Mən xüsusilə triqonometrik düsturlara diqqət yetirirəm, onlar sizin gözünüzün qabağında olmalıdırlar- bu olmadan iş səmərəliliyi nəzərəçarpacaq dərəcədə azalacaq.

Ancaq əvvəlcə bu məqalədə inteqralların nə olduğu haqqında Yox. Formanın inteqralları yoxdur, - kosinus, sinus, bəzi polinomla vurulur (daha az tez-tez tangens və ya kotangens olan bir şey). Belə inteqrallar hissələrlə inteqral edilir və metodu öyrənmək üçün hissələrə görə inteqrasiya dərsinə baş çəkin. Həll nümunələri.Həmçinin burada “tağları” olan inteqrallar yoxdur - arktangens, arksinus və s., Onlar da çox vaxt hissələrlə inteqrasiya olunur.

Triqonometrik funksiyaların inteqrallarını taparkən bir sıra üsullardan istifadə olunur:

(4) Cədvəl formulundan istifadə edirik , yeganə fərq odur ki, “X” əvəzinə mürəkkəb ifadəmiz var.

Misal 2

Misal 3

Qeyri-müəyyən inteqralı tapın.

Müsabiqədə boğulanlar üçün janrın klassiki. Yəqin ki, qeyd etdiyiniz kimi, inteqrallar cədvəlində tangens və kotangensin inteqralı yoxdur, lakin buna baxmayaraq, belə inteqralları tapmaq olar.

(1) Biz triqonometrik düsturdan istifadə edirik

(2) Funksiyanı diferensial işarənin altına gətiririk.

(3) Cədvəl inteqralından istifadə edirik .

Misal 4

Qeyri-müəyyən inteqralı tapın.

Bu müstəqil həll nümunəsidir, tam həll və cavab dərsin sonundadır.

Misal 5

Qeyri-müəyyən inteqralı tapın.

Dərəcələrimiz tədricən artacaq =).
Əvvəlcə həll yolu:

(1) Düsturdan istifadə edirik

(2) Biz əsas triqonometrik eynilikdən istifadə edirik , bundan belə çıxır .

(3) Hissəni məxrəc termininə bölün.

(4) Biz qeyri-müəyyən inteqralın xətti xüsusiyyətindən istifadə edirik.

(5) Cədvəldən istifadə edərək inteqrasiya edirik.

Misal 6

Qeyri-müəyyən inteqralı tapın.

Bu müstəqil həll nümunəsidir, tam həll və cavab dərsin sonundadır.

Daha yüksək güclərdə olan tangens və kotangentlərin inteqralları da var. Dərsdə tangens kubunun inteqralı müzakirə olunur Düz bir fiqurun sahəsini necə hesablamaq olar? Dördüncü və beşinci dərəcələrə toxunan (kotangens) inteqrallarını səhifədə əldə etmək olar. Kompleks inteqrallar.

İnteqralın dərəcəsinin azaldılması

Bu texnika inteqral funksiyalar sinus və kosinuslarla doldurulduqda işləyir hətta dərəcə. Dərəcəni azaltmaq üçün triqonometrik düsturlardan istifadə edin , və , və sonuncu düstur tez-tez əks istiqamətdə istifadə olunur: .

Misal 7

Qeyri-müəyyən inteqralı tapın.

Həll:

Prinsipcə, burada düsturu tətbiq etməyimizdən başqa heç bir yenilik yoxdur (inteqralın dərəcəsinin aşağı salınması). Nəzərə alın ki, mən həlli qısaltmışam. Təcrübə qazandıqca inteqral şifahi olaraq tapıla bilər; bu, vaxta qənaət edir və tapşırıqları bitirərkən olduqca məqbuldur. Bu halda qaydanı təsvir etməmək məsləhətdir , əvvəlcə şifahi olaraq 1-in, sonra -nın inteqralını alırıq.

Misal 8

Qeyri-müəyyən inteqralı tapın.

Bu müstəqil həll nümunəsidir, tam həll və cavab dərsin sonundadır.

Bu vəd edilən dərəcə artımıdır:

Misal 9

Qeyri-müəyyən inteqralı tapın.

Əvvəlcə həll yolu, sonra şərhlər:

(1) Düsturu tətbiq etmək üçün inteqran hazırlayın .

(2) Biz əslində düsturu tətbiq edirik.

(3) Məxrəci kvadrata çəkirik və sabiti inteqral işarəsindən çıxarırıq. Bir az başqa cür də edilə bilərdi, amma fikrimcə, daha rahat idi.

(4) Düsturdan istifadə edirik

(5) Üçüncü termində dərəcəni yenidən azaldırıq, lakin düsturdan istifadə edirik .

(6) Biz oxşar terminləri təqdim edirik (burada termini terminə böldüm və əlavə etdi).

(7) Əslində, biz inteqralı, xəttilik qaydasını götürürük funksiyanın diferensial işarəsi altında cəmlənməsi üsulu isə şifahi şəkildə yerinə yetirilir.

(8) Cavabın birləşdirilməsi.

! Qeyri-müəyyən inteqralda cavab çox vaxt bir neçə şəkildə yazıla bilər

İndicə nəzərdən keçirilən nümunədə son cavab fərqli şəkildə yazıla bilərdi - mötərizələri açmaq və hətta ifadəni inteqrasiya etməzdən əvvəl bunu etmək, yəni nümunənin aşağıdakı sonluğu olduqca məqbuldur:

Bu seçimin daha rahat olması olduqca mümkündür, mən bunu özüm həll etməyə öyrəşdiyim şəkildə izah etdim). Müstəqil bir həll üçün başqa bir tipik nümunə:

Misal 10

Qeyri-müəyyən inteqralı tapın.

Bu nümunəni iki yolla həll etmək olar və siz uğur qazana bilərsiniz iki tamamilə fərqli cavab(daha doğrusu, onlar tamamilə fərqli görünəcəklər, lakin riyazi baxımdan ekvivalent olacaqlar). Çox güman ki, ən rasional metodu görməyəcəksiniz və mötərizələri açmaq və digər triqonometrik düsturlardan istifadə etməklə əziyyət çəkəcəksiniz. Ən təsirli həll dərsin sonunda verilir.

Paraqrafı ümumiləşdirmək üçün belə bir nəticəyə gəlirik: formanın hər hansı bir inteqralı , harada və - həttaədədlər, inteqralın dərəcəsini azaltma üsulu ilə həll edilir.
Təcrübədə 8 və 10 dərəcə olan inteqrallarla qarşılaşdım və dərəcəni bir neçə dəfə aşağı salmaqla onların dəhşətli qarışıqlığını həll etməli oldum, nəticədə uzun, uzun cavablar aldım.

Dəyişənlərin dəyişdirilməsi metodu

Məqalədə qeyd edildiyi kimi Qeyri-müəyyən inteqralda dəyişən dəyişmə üsulu, əvəzetmə metodundan istifadə üçün əsas şərt inteqralda müəyyən bir funksiyanın və onun törəməsinin olmasıdır:
(funksiyalar mütləq məhsulda deyil)

Misal 11

Qeyri-müəyyən inteqralı tapın.

Törəmələr cədvəlinə baxırıq və düsturlara diqqət yetiririk, , yəni bizim inteqranımızda funksiya və onun törəməsi var. Lakin biz görürük ki, diferensiallaşma zamanı kosinus və sinus qarşılıqlı olaraq bir-birinə çevrilir və belə bir sual yaranır: dəyişənin dəyişməsini necə yerinə yetirmək olar və sinus və ya kosinus dedikdə nəyi nəzərdə tuturuq?! Sualı elmi poking ilə həll etmək olar: əgər dəyişdirməni səhv yerinə yetirsək, onda yaxşı bir şey olmayacaq.

Ümumi təlimat: oxşar hallarda məxrəcdə olan funksiyanı təyin etməlisiniz.

Biz həlli dayandırırıq və əvəz edirik

Məxrəcdə hər şey yaxşıdır, hər şey yalnız asılıdır , indi onun nəyə çevriləcəyini tapmaq qalır.
Bunun üçün diferensial tapırıq:

Və ya qısaca:
Yaranan bərabərlikdən, nisbət qaydasından istifadə edərək, ehtiyacımız olan ifadəni ifadə edirik:

Belə ki:

İndi bizim bütün inteqralımız yalnız ondan asılıdır və biz həll etməyə davam edə bilərik

Hazır. Nəzərinizə çatdırım ki, əvəzetmənin məqsədi inteqrandı sadələşdirməkdir, bu vəziyyətdə hər şey güc funksiyasını cədvələ uyğun inteqrasiya etməyə gəldi.

Təsadüfi deyil ki, bu nümunəni bu qədər ətraflı təsvir etdim, bu, dərs materiallarının təkrarlanması və möhkəmləndirilməsi məqsədi ilə edildi. Qeyri-müəyyən inteqralda dəyişən dəyişmə üsulu.

İndi öz həlliniz üçün iki nümunə:

Misal 12

Qeyri-müəyyən inteqralı tapın.

Misal 13

Qeyri-müəyyən inteqralı tapın.

Dərsin sonunda həllər və cavabları tamamlayın.

Misal 14

Qeyri-müəyyən inteqralı tapın.

Burada yenə inteqralda sinus və kosinus var (törəmə ilə funksiya), lakin hasildə və dilemma yaranır - sinus və ya kosinus dedikdə nəyi nəzərdə tuturuq?

Elmi metoddan istifadə edərək dəyişdirmə aparmağa cəhd edə bilərsiniz və heç bir şey işləmirsə, onu başqa bir funksiya kimi təyin edin, amma var:

Ümumi göstəriş: məcazi mənada desək, "narahat vəziyyətdə" olan funksiyanı təyin etməlisiniz..

Bu misalda tələbə kosinusunun dərəcədən “əziyyət çəkdiyini”, sinusun isə sərbəst oturduğunu görürük.

Buna görə də bir əvəz edək:

Əgər hər kəs dəyişəni əvəz etmək və diferensial tapmaq alqoritmi ilə hələ də çətinlik çəkirsə, onda siz dərsə qayıtmalısınız. Qeyri-müəyyən inteqralda dəyişən dəyişmə üsulu.

Misal 15

Qeyri-müəyyən inteqralı tapın.

İnteqrandı təhlil edək, nə ilə işarələnməlidir?
Təlimatlarımızı xatırlayaq:
1) Funksiya çox güman ki, məxrəcdədir;
2) Funksiya “əlverişsiz vəziyyətdə”dir.

Yeri gəlmişkən, bu təlimatlar təkcə triqonometrik funksiyalar üçün keçərli deyil.

Sinus hər iki meyara (xüsusilə də ikinci) uyğun gəlir, buna görə də əvəzetmə özünü göstərir. Prinsipcə, dəyişdirmə artıq həyata keçirilə bilər, amma əvvəlcə nə edəcəyinizi anlamaq yaxşı olardı? Əvvəlcə bir kosinusu “çimdikləyirik”:

Biz “gələcək” diferensialımızı ehtiyatda saxlayırıq

Və biz bunu əsas triqonometrik eynilikdən istifadə edərək sinus vasitəsilə ifadə edirik:

İndi əvəzetmə budur:

Ümumi qayda: Əgər inteqralda triqonometrik funksiyalardan biri (sinus və ya kosinus) olarsa qəribə dərəcə, onda siz tək dərəcədən bir funksiyanı “dişləyib” onun arxasında başqa bir funksiya təyin etməlisiniz. Söhbət yalnız kosinusların və sinusların olduğu inteqrallardan gedir.

Nəzərdən keçirilən nümunədə tək gücdə bir kosinusumuz var idi, ona görə də gücdən bir kosinus çıxardıq və onu sinus kimi təyin etdik.

Misal 16

Qeyri-müəyyən inteqralı tapın.

Dərəcələr qalxır =).
Bu, özünüz həll etməyiniz üçün bir nümunədir. Tam həll və dərsin sonunda cavab.

Universal triqonometrik əvəzetmə

Universal triqonometrik əvəzetmə dəyişənlərin dəyişdirilməsi metodunun ümumi halıdır. “Nə edəcəyinizi bilməyəndə” ondan istifadə etməyə cəhd edə bilərsiniz. Ancaq əslində onun tətbiqi üçün bəzi qaydalar var. Universal triqonometrik əvəzetmənin tətbiq edilməli olduğu tipik inteqrallar aşağıdakı inteqrallardır: , , , və s.

Misal 17

Qeyri-müəyyən inteqralı tapın.

Bu halda universal triqonometrik əvəzetmə aşağıdakı şəkildə həyata keçirilir. Əvəz edək: . Mən hərfdən istifadə etmirəm, amma məktub, bu bir növ qayda deyil, sadəcə olaraq, yenə də mən hər şeyi bu şəkildə həll etməyə öyrəşmişəm.

Burada diferensial tapmaq daha rahatdır, bunun üçün bərabərlikdən ifadə edirəm:
Mən hər iki hissəyə arktangent əlavə edirəm:

Arktangens və tangens bir-birini ləğv edir:

Beləliklə:

Praktikada onu bu qədər təfərrüatlı şəkildə təsvir etmək lazım deyil, sadəcə hazır nəticədən istifadə edin:

! İfadə yalnız sinusların və kosinusların altında inteqral üçün sadəcə “X” varsa etibarlıdır. (bu haqda daha sonra danışacağıq) hər şey bir az fərqli olacaq!

Əvəz edərkən sinuslar və kosinuslar aşağıdakı fraksiyalara çevrilir:
, , bu bərabərliklər tanınmış triqonometrik düsturlara əsaslanır: ,

Beləliklə, son dizayn belə görünə bilər:

Universal triqonometrik əvəzləmə aparaq:

Özünüz həll etməli olduğunuz, cavablarını görə biləcəyiniz problemlər də olacaq.

İnteqral triqonometrik funksiyaların hasilindən cəminə çevrilə bilər

Gəlin, inteqralın sinusların və x-in birinci dərəcəli kosinuslarının müxtəlif amillərə vurulması nəticəsində yaranan inteqralları, yəni formanın inteqrallarını nəzərdən keçirək.

Tanınmış triqonometrik düsturlardan istifadə etməklə

(2)
(3)
(4)
(31) formasının inteqrallarında hasillərin hər birini cəbri cəmiyə çevirmək və düsturlara uyğun olaraq inteqrasiya etmək olar

(5)

(6)

Misal 1. Tapın

Həll. Formula (2) uyğun olaraq

Misal 2. Tapın triqonometrik funksiyanın inteqralı

Həll. Formula (3) uyğun olaraq

Misal 3. Tapın triqonometrik funksiyanın inteqralı

Həll. Formula (4) uyğun olaraq inteqralın aşağıdakı çevrilməsini əldə edirik:

Formula (6) tətbiq edərək, əldə edirik

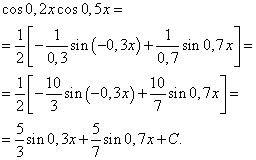
Eyni arqumentin sinus və kosinus güclərinin hasilinin inteqralı

İndi eyni arqumentin sinusunun və kosinusunun güclərinin məhsulu olan funksiyaların inteqrallarını nəzərdən keçirək, yəni.

(7)

Xüsusi hallarda göstəricilərdən biri ( m və ya n) sıfır ola bilər.

Bu cür funksiyaları birləşdirərkən istifadə olunur ki, kosinusun bərabər qüvvəsi sinus vasitəsilə ifadə edilə bilər və sinusun diferensialı cos-a bərabərdir. x dx(və ya hətta sinusun gücü kosinusla ifadə edilə bilər və kosinusun diferensialı - sinə bərabərdir. x dx ) .

İki halı fərqləndirmək lazımdır: 1) göstəricilərdən ən azı biri m Və n qəribə; 2) hər iki göstərici cütdür.

Birinci hal baş versin, yəni göstərici n = 2k+ 1 - tək. Sonra bunu nəzərə alaraq

İnteqral elə təqdim olunur ki, onun bir hissəsi yalnız sinusun funksiyası, digəri isə sinusun diferensialıdır. İndi dəyişən əvəz istifadə edir t= günah x həll çoxhədlinin inteqralına endirilir t. Yalnız dərəcə m qəribədirsə, günah amilini təcrid edərək eyni şeyi edirlər x, inteqranın qalan hissəsini cos ilə ifadə edir x və inanmaq t= cos x. Bu texnikadan da istifadə oluna bilər sinus və kosinusun bölmə səlahiyyətlərinin inteqrasiyası , Nə vaxt göstəricilərdən ən azı biri təkdir . Bütün məsələ ondadır sinus və kosinusun güclərinin nisbəti onların hasilinin xüsusi halıdır : Triqonometrik funksiya inteqralın məxrəcində olduqda onun dərəcəsi mənfi olur. Lakin qismən triqonometrik funksiyaların səlahiyyətləri yalnız cüt olduqda halları da var. Onlar haqqında - növbəti paraqrafda.

Hər iki göstərici varsa m Və n– hətta, onda triqonometrik düsturlardan istifadə etməklə

sinus və kosinusun eksponentlərini azaldın, bundan sonra yuxarıdakı kimi eyni tipli inteqral alınır. Ona görə də inteqrasiya eyni sxem üzrə davam etdirilməlidir. Əgər cüt göstəricilərdən biri mənfi olarsa, yəni sinus və kosinusun cüt qüvvələrinin nisbəti nəzərə alınarsa, bu sxem uyğun deyil. . Sonra inteqralın necə çevrilə biləcəyindən asılı olaraq dəyişənin dəyişməsindən istifadə edilir. Belə bir işə növbəti paraqrafda baxılacaqdır.

Misal 4. Tapın triqonometrik funksiyanın inteqralı

Həll. Kosinus eksponenti təkdir. Buna görə də təsəvvür edək

t= günah x(Sonra dt= cos x dx ). Sonra alırıq

Köhnə dəyişənə qayıdaraq nəhayət tapırıq

Misal 5. Tapın triqonometrik funksiyanın inteqralı

.

Həll. Kosinus eksponenti, əvvəlki nümunədə olduğu kimi, təkdir, lakin daha böyükdür. Təsəvvür edək

və dəyişən dəyişikliyi edin t= günah x(Sonra dt= cos x dx ). Sonra alırıq

Mötərizələri açaq

və alırıq

Köhnə dəyişənə qayıdaraq, həllini əldə edirik

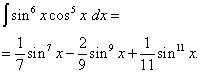
Misal 6. Tapın triqonometrik funksiyanın inteqralı

Həll. Sinus və kosinusun göstəriciləri cütdür. Beləliklə, inteqral funksiyanı aşağıdakı kimi çeviririk:

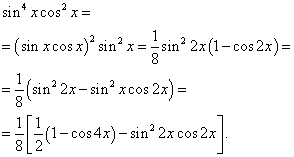
Sonra alırıq

İkinci inteqralda dəyişən dəyişikliyi edirik, təyin edirik t= günah2 x. Sonra (1/2)dt= cos2 x dx . Beləliklə,

Nəhayət alırıq

Dəyişənlərin dəyişdirilməsi metodundan istifadə

Dəyişənlərin dəyişdirilməsi metodu triqonometrik funksiyaları birləşdirərkən, inteqralda yalnız sinus və ya yalnız kosinus, sinus və ya kosinusun birinci dərəcədə olduğu, tangens və ya kotangens olan sinus və kosinusun hasilini, habelə əmsalın bölünməsini ehtiva etdiyi hallarda istifadə edilə bilər. hətta bir və eyni arqumentin sinus və kosinus gücləri. Bu halda, yalnız günah deyil, permutasiya etmək mümkündür x = t və günah x = t, həm də tg x = t və ctg x = t .

Misal 8. Tapın triqonometrik funksiyanın inteqralı

.

Həll. Gəlin dəyişəni dəyişdirək: , sonra . Yaranan inteqral inteqrallar cədvəlindən istifadə etməklə asanlıqla inteqrasiya oluna bilər:

.

Misal 9. Tapın triqonometrik funksiyanın inteqralı

Həll. Tangensi sinus və kosinus nisbətinə çevirək:

Gəlin dəyişəni dəyişdirək: , sonra . Nəticə inteqraldır cədvəl inteqralı mənfi işarə ilə:

.

Orijinal dəyişənə qayıdaraq nəhayət əldə edirik:

.

Misal 10. Tapın triqonometrik funksiyanın inteqralı

Həll. Gəlin dəyişəni dəyişdirək: , sonra .

Triqonometrik eyniliyi tətbiq etmək üçün inteqranı çevirək :

İnteqralın qarşısına mənfi işarə qoymağı unutmadan dəyişəni dəyişdiririk (yuxarıya baxın, nəyə bərabərdir? dt). Sonra, inteqranı faktorlara ayırırıq və cədvələ uyğun olaraq inteqrasiya edirik:

Orijinal dəyişənə qayıdaraq nəhayət əldə edirik:

.

Triqonometrik funksiyanın inteqralını özünüz tapın və həllinə baxın

Universal triqonometrik əvəzetmə

Universal triqonometrik əvəzetmə inteqralın əvvəlki bəndlərdə müzakirə olunan hallara aid olmadığı hallarda istifadə edilə bilər. Əsasən, sinus və ya kosinus (və ya hər ikisi) kəsrin məxrəcində olduqda. Sübut edilmişdir ki, sinus və kosinusu orijinal bucağın yarısının tangensini ehtiva edən başqa bir ifadə ilə aşağıdakı kimi əvəz etmək olar:

Ancaq unutmayın ki, universal triqonometrik əvəzetmə çox vaxt olduqca mürəkkəb cəbri çevrilmələrə səbəb olur, buna görə də başqa heç bir üsul işləməyəndə istifadə etmək daha yaxşıdır. Universal triqonometrik əvəzetmə ilə birlikdə diferensial işarə altında əvəzetmə və qeyri-müəyyən əmsallar üsulundan istifadə edilən nümunələrə baxaq.

Misal 12. Tapın triqonometrik funksiyanın inteqralı

.

Həll. Həll. Gəlin yararlanaq universal triqonometrik əvəzetmə. Sonra
.

Hissədə və məxrəcdə olan kəsrləri vurub ikisini çıxarıb inteqral işarəsinin qarşısına qoyuruq. Sonra

İnteqralların hissələr üzrə həlli nümunələri ətraflı nəzərdən keçirilir, onların inteqranı çoxhədlinin eksponensial (e-nin x gücünə) və ya sinusun (sin x) və ya kosinusun (cos x) məhsuludur.

Həmçinin bax: Parçalar üzrə inteqrasiya üsulu
Qeyri-müəyyən inteqrallar cədvəli
Qeyri-müəyyən inteqralların hesablanması üsulları
Əsas elementar funksiyalar və onların xassələri

Hissələr üzrə inteqrasiya düsturu

Bu bölmədəki nümunələri həll edərkən hissələrə görə inteqrasiya düsturu istifadə olunur:
;
.

Çoxhədli və sin x, cos x və ya e x hasilini ehtiva edən inteqral nümunələri

Bu cür inteqralların nümunələri:
, , .

Belə inteqralları inteqral etmək üçün çoxhədli u, qalan hissəsi isə v dx ilə işarələnir. Sonra, hissələrə görə inteqrasiyanı tətbiq edin.

Aşağıda bu nümunələrin ətraflı həlli verilmişdir.

İnteqralların həlli nümunələri

X-in gücünə e eksponentli misal

İnteqralı təyin edin:
.

Diferensial işarəsi altında eksponent təqdim edək:
e - x dx = - e - x d(-x) = - d(e - x).

Gəlin hissələrə görə inteqrasiya edək.

Budur
.
Qalan inteqralı da hissələrə görə birləşdiririk.
.
.
.
Nəhayət bizdə:
.

Sinus ilə inteqralın təyin edilməsinə nümunə

İnteqralı hesablayın:
.

Diferensial işarəsi altında sinüsü təqdim edək:

Gəlin hissələrə görə inteqrasiya edək.

burada u = x 2, v = cos(2 x+3), du = ( x 2 )′ dx

Qalan inteqralı da hissələrə görə birləşdiririk. Bunun üçün diferensial işarənin altında kosinusu təqdim edin.


burada u = x, v = günah(2 x+3), du = dx

Nəhayət bizdə:

Çoxhədli və kosinusun hasilinə nümunə

İnteqralı hesablayın:
.

Diferensial işarəsi altında kosinusu təqdim edək:

Gəlin hissələrə görə inteqrasiya edək.

burada u = x 2 + 3 x + 5, v = günah 2 x, du = ( x 2 + 3 x + 5 )′ dx

Kompleks inteqrallar

Bu məqalə qeyri-müəyyən inteqrallar mövzusunu yekunlaşdırır və kifayət qədər mürəkkəb hesab etdiyim inteqralları ehtiva edir. Dərs daha çətin nümunələrin saytda təhlil edilməsini arzulayan ziyarətçilərin təkrar müraciəti əsasında yaradılmışdır.

Güman edilir ki, bu mətnin oxucusu yaxşı hazırlanmışdır və əsas inteqrasiya üsullarını necə tətbiq edəcəyini bilir. Dummies və inteqrallara çox arxayın olmayan insanlar ilk dərsə müraciət etməlidirlər - Qeyri-müəyyən inteqral. Həll nümunələri, burada mövzunu demək olar ki, sıfırdan mənimsəyə bilərsiniz. Daha təcrübəli tələbələr mənim məqalələrimdə hələ rast gəlinməyən inteqrasiya üsulları və üsulları ilə tanış ola bilərlər.

Hansı inteqrallar nəzərə alınacaq?

Əvvəlcə həlli üçün ardıcıl olaraq istifadə etdiyimiz kökləri olan inteqralları nəzərdən keçirəcəyik dəyişən əvəz Və hissələri ilə inteqrasiya. Yəni bir misalda iki texnika eyni vaxtda birləşdirilir. Və daha çox.

Sonra maraqlı və orijinal ilə tanış olacağıq inteqralı özünə endirmə üsulu. Kifayət qədər bir neçə inteqral bu şəkildə həll olunur.

Proqramın üçüncü buraxılışı əvvəlki məqalələrdə kassanın yanından keçən mürəkkəb fraksiyaların inteqralları olacaq.

Dördüncüsü, triqonometrik funksiyalardan əlavə inteqrallar təhlil ediləcək. Xüsusilə, çox vaxt aparan universal triqonometrik əvəzləmədən qaçan üsullar var.

(2) İnteqral funksiyasında payı məxrəcə görə hədlərə bölürük.

(3) Biz qeyri-müəyyən inteqralın xətti xüsusiyyətindən istifadə edirik. Dərhal sonuncu inteqralda funksiyanı diferensial işarənin altına qoyun.

(4) Qalan inteqralları götürürük. Qeyd edək ki, loqarifmdə moduldan çox mötərizələrdən istifadə edə bilərsiniz, çünki .

(5) Birbaşa əvəzdən "te" ifadə edərək tərs dəyişdirmə həyata keçiririk:

Mazoşist tələbələr cavabı fərqləndirə və mənim etdiyim kimi orijinal inteqrandı əldə edə bilərlər. Xeyr, yox, mən düzgün mənada yoxlama etdim =)

Gördüyünüz kimi, həll zamanı biz ikidən çox həll metodundan istifadə etməli olduq, ona görə də belə inteqrallarla məşğul olmaq üçün sizə inamlı inteqrasiya bacarıqları və kifayət qədər təcrübə lazımdır.

Praktikada, əlbəttə ki, kvadrat kök daha çox yayılmışdır, onu özünüz həll etmək üçün üç nümunə var:

Misal 2

Qeyri-müəyyən inteqralı tapın

Misal 3

Qeyri-müəyyən inteqralı tapın

Misal 4

Qeyri-müəyyən inteqralı tapın

Bu nümunələr eyni tiplidir, ona görə də məqalənin sonundakı tam həll yalnız 2-ci Nümunə üçün olacaq; Nümunələr 3-4-də eyni cavablar var. Qərarların əvvəlində hansı əvəzedicinin istifadə ediləcəyi, məncə, göz qabağındadır. Niyə eyni tipli nümunələri seçdim? Tez-tez onların rolunda tapılır. Daha tez-tez, bəlkə də, sadəcə bir şey kimi .

Ancaq həmişə deyil, arktangens, sinus, kosinus, eksponensial və digər funksiyaların altında xətti funksiyanın kökü olduqda, bir anda bir neçə üsuldan istifadə etmək lazımdır. Bir sıra hallarda, "asanlıqla çıxmaq" mümkündür, yəni dəyişdirildikdən dərhal sonra asanlıqla götürülə bilən sadə bir inteqral əldə edilir. Yuxarıda təklif olunan tapşırıqların ən asanı Nümunə 4-dür, burada əvəz edildikdən sonra nisbətən sadə inteqral alınır.

İnteqralı özünə endirməklə

Ağıllı və gözəl bir üsul. Bu janrın klassiklərinə nəzər salaq:

Misal 5

Qeyri-müəyyən inteqralı tapın

Kökün altında kvadratik binomial var və bu nümunəni inteqrasiya etməyə çalışmaq çaydanı saatlarla baş ağrısına səbəb ola bilər. Belə bir inteqral hissələrə bölünür və özünə endirilir. Prinsipcə, çətin deyil. Bilirsən necə.

Baxılan inteqralı latın hərfi ilə işarə edək və həllinə başlayaq:

Gəlin hissələrə görə inteqrasiya edək:

(1) Müddətə bölünmə üçün inteqral funksiyanı hazırlayın.

(2) İnteqral funksiya terminini terminə bölürük. Hər kəs üçün aydın olmaya bilər, amma mən bunu daha ətraflı təsvir edəcəyəm:

(3) Biz qeyri-müəyyən inteqralın xətti xüsusiyyətindən istifadə edirik.

(4) Sonuncu inteqralı ("uzun" loqarifmini) götürün.

İndi həllin ən başlanğıcına baxaq:

Və sonunda:

Nə olub? Manipulyasiyalarımız nəticəsində inteqral özünə endirildi!

Gəlin əvvəli və sonunu bərabərləşdirək:

İşarə dəyişikliyi ilə sola keçin:

Və ikisini sağ tərəfə keçirik. Nəticə olaraq:

Sabit, daha dəqiq desək, əvvəllər əlavə edilməli idi, amma sonunda əlavə etdim. Burada sərtliyin nə olduğunu oxumağı şiddətlə tövsiyə edirəm:

Qeyd: Daha dəqiq desək, həllin son mərhələsi belə görünür:

Beləliklə:

Sabit yenidən təyin edilə bilər. Niyə yenidən təyin oluna bilər? Çünki o, hələ də bunu qəbul edir hər hansı dəyərlərdir və bu mənada sabitlər arasında heç bir fərq yoxdur.
Nəticə olaraq:

Daimi renotasiya ilə oxşar hiylə geniş istifadə olunur diferensial tənliklər. Və orada mən sərt olacağam. Və burada mən bu cür azadlığa yalnız sizi lazımsız şeylərlə qarışdırmamaq və diqqəti inteqrasiya metodunun özünə yönəltmək üçün icazə verirəm.

Misal 6

Qeyri-müəyyən inteqralı tapın

Müstəqil həll üçün başqa tipik inteqral. Tam həll və dərsin sonunda cavab. Əvvəlki nümunədəki cavabla fərq olacaq!

Kvadrat kökün altında kvadrat trinomial varsa, hər halda həll iki təhlil edilmiş nümunəyə gəlir.

Məsələn, inteqralı nəzərdən keçirək . Sizə lazım olan hər şey birincidir tam kvadrat seçin:
.
Sonra, "heç bir nəticə vermədən" bir xətti dəyişdirmə aparılır:
, nəticədə inteqral alınır. Tanış bir şey, elə deyilmi?

Və ya kvadrat binomial ilə bu nümunə:
Tam kvadrat seçin:
Və xətti əvəz etdikdən sonra biz artıq müzakirə olunan alqoritmdən istifadə edərək həll olunan inteqralı alırıq.

İnteqralı özünə necə azaltmağın daha iki tipik nümunəsinə baxaq:
– eksponensialın sinusla vurulan inteqralı;
– eksponensialın kosinusu ilə vurulan inteqralı.

Hissələr üzrə sadalanan inteqrallarda siz iki dəfə inteqrasiya etməli olacaqsınız:

Misal 7

Qeyri-müəyyən inteqralı tapın

İnteqral eksponensialın sinusla vurulmasıdır.

Biz hissələrə görə iki dəfə inteqrasiya edirik və inteqralı özünə endiririk:

Hissələr üzrə ikiqat inteqrasiya nəticəsində inteqral özünə endirildi. Həllin başlanğıcını və sonunu bərabərləşdiririk:

İşarə dəyişikliyi ilə onu sol tərəfə keçiririk və inteqralımızı ifadə edirik:

Hazır. Eyni zamanda, sağ tərəfi daramaq məsləhətdir, yəni. eksponenti mötərizədən çıxarın və sinus və kosinusu mötərizədə “gözəl” ardıcıllıqla yerləşdirin.

İndi nümunənin əvvəlinə, daha dəqiq desək, hissələr üzrə inteqrasiyaya qayıdaq:

Biz eksponent kimi təyin etdik. Sual yaranır: həmişə ilə işarələnməli olan eksponentdirmi? Lazım deyil. Əslində, nəzərdən keçirilən inteqralda əsaslı olaraq fərq etməz, dedikdə nəyi nəzərdə tuturuq, başqa yolla gedə bilərdik:

Bu niyə mümkündür? Eksponensial özünə çevrildiyi üçün (həm diferensiallaşma, həm də inteqrasiya zamanı), sinus və kosinus qarşılıqlı olaraq bir-birinə çevrilir (yenə də həm diferensiallaşma, həm də inteqrasiya zamanı).

Yəni triqonometrik funksiyanı da işarələyə bilərik. Ancaq nəzərdən keçirilən nümunədə bu, daha az rasionaldır, çünki fraksiyalar görünəcəkdir. İstəyirsinizsə, bu nümunəni ikinci üsuldan istifadə edərək həll etməyə cəhd edə bilərsiniz, cavablar uyğun olmalıdır.

Misal 8

Qeyri-müəyyən inteqralı tapın

Bu, özünüz həll etməyiniz üçün bir nümunədir. Qərar verməzdən əvvəl düşünün, bu halda eksponensial və ya triqonometrik funksiya kimi təyin etmək daha sərfəlidir? Tam həll və dərsin sonunda cavab.

Əlbətdə ki, bu dərsdəki cavabların əksəriyyətini fərqləndirmə ilə yoxlamaq olduqca asan olduğunu unutmayın!

Baxılan nümunələr ən mürəkkəb deyildi. Təcrübədə inteqrallar sabitin həm eksponentdə, həm də triqonometrik funksiyanın arqumentində olduğu yerlərdə daha çox yayılmışdır, məsələn: . Bir çox insanlar belə bir inteqralda çaşacaqlar və mən də tez-tez özümü çaşdırıram. Fakt budur ki, məhlulda fraksiyaların görünmə ehtimalı yüksəkdir və ehtiyatsızlıqdan nəyisə itirmək çox asandır. Bundan əlavə, işarələrdə səhv olma ehtimalı yüksəkdir; nəzərə alın ki, eksponentin mənfi işarəsi var və bu, əlavə çətinlik yaradır.

Son mərhələdə nəticə çox vaxt belə olur:

Həllin sonunda belə, son dərəcə diqqətli olmalı və fraksiyaları düzgün başa düşməlisiniz:

Kompleks Fraksiyaların İnteqrasiya Edilməsi

Biz yavaş-yavaş dərsin ekvatoruna yaxınlaşırıq və fraksiyaların inteqrallarını nəzərdən keçirməyə başlayırıq. Yenə də, onların hamısı super mürəkkəb deyil, sadəcə olaraq bu və ya digər səbəbdən nümunələr digər məqalələrdə bir az “mövzudan kənar” idi.

Köklər mövzusunun davamı

Misal 9

Qeyri-müəyyən inteqralı tapın

Kökün altındakı məxrəcdə kvadrat üçbucaq üstəgəl kökdən kənarda “X” şəklində “əlavə” var. Bu tip inteqral standart əvəzetmə ilə həll edilə bilər.

Qərar veririk:

Burada dəyişdirmə sadədir:

Əvəz olunduqdan sonra həyata baxaq:

(1) Əvəz etdikdən sonra kök altındakı şərtləri ortaq məxrəcə endiririk.
(2) Kökün altından çıxarırıq.
(3) Say və məxrəc ilə azaldılır. Eyni zamanda, kökün altında, şərtləri uyğun bir sıra ilə yenidən düzəltdim. Müəyyən təcrübə ilə, şərh edilən hərəkətləri şifahi olaraq yerinə yetirməklə (1), (2) addımları atlaya bilərsiniz.
(4) Nəticə inteqral, dərsdən xatırladığınız kimi Bəzi Kəsrlərin İnteqrasiyası, qərara alınır tam kvadrat çıxarma üsulu. Tam kvadrat seçin.
(5) İnteqrasiya yolu ilə biz adi “uzun” loqarifm alırıq.
(6) Biz tərs dəyişdirmə həyata keçiririk. Əgər əvvəlcə , sonra geri: .
(7) Son hərəkət nəticəni düzəltməyə yönəlib: kök altında biz yenidən terminləri ortaq məxrəcə gətiririk və onları kökün altından çıxarırıq.

Misal 10

Qeyri-müəyyən inteqralı tapın

Bu, özünüz həll etməyiniz üçün bir nümunədir. Burada tək "X" ə bir sabit əlavə olunur və əvəzetmə demək olar ki, eynidir:

Əlavə etməli olduğunuz yeganə şey yerinə yetirilən əvəzdən "x" ifadə etməkdir:

Tam həll və dərsin sonunda cavab.

Bəzən belə inteqralda kök altında kvadrat binom ola bilər, bu həll üsulunu dəyişmir, daha da sadə olacaqdır. Fərqi hiss edin:

Misal 11

Qeyri-müəyyən inteqralı tapın

Misal 12

Qeyri-müəyyən inteqralı tapın

Dərsin sonunda qısa həllər və cavablar. Qeyd etmək lazımdır ki, Nümunə 11 dəqiqdir binom inteqral, həll üsulu sinifdə müzakirə edilmişdir İrrasional funksiyaların inteqralları.

2-ci dərəcəli ayrılmaz çoxhədlinin gücünə inteqralı

(məxrəcdə çoxhədli)

Daha nadir inteqral növü, lakin buna baxmayaraq praktiki nümunələrdə rast gəlinir.

Misal 13

Qeyri-müəyyən inteqralı tapın

Ancaq 13 nömrəli şanslı nümunəyə qayıdaq (düzünü desəm, düzgün təxmin etmədim). Bu inteqral həm də necə həll edəcəyinizi bilmirsinizsə, olduqca sinir bozucu ola biləcəklərdən biridir.

Həll süni çevrilmə ilə başlayır:

Düşünürəm ki, hər kəs payı məxrəcə görə terminə bölməyi artıq başa düşür.

Yaranan inteqral hissələrə bölünür:

Formanın inteqralı üçün ( – natural ədəd) əldə edirik təkrarlanan azalma düsturu:
, Harada – bir dərəcə aşağı inteqral.

Həll olunmuş inteqral üçün bu düsturun doğruluğunu yoxlayaq.
Bu halda: , , düsturundan istifadə edirik:

Gördüyünüz kimi, cavablar eynidir.

Misal 14

Qeyri-müəyyən inteqralı tapın

Bu, özünüz həll etməyiniz üçün bir nümunədir. Nümunə həlli yuxarıdakı düsturdan ardıcıl olaraq iki dəfə istifadə edir.

Əgər dərəcə altındadırsa bölünməz kvadrat trinomial, sonra mükəmməl kvadratı təcrid etməklə həll binomiala endirilir, məsələn:

Numeratorda əlavə çoxhədli olarsa necə? Bu zaman qeyri-müəyyən əmsallar üsulundan istifadə edilir və inteqral funksiyası kəsrlərin cəminə genişləndirilir. Amma mənim təcrübəmdə belə bir nümunə var heç görüşməmişəm, buna görə də məqalədə bu işi qaçırdım Kəsr-rasional funksiyaların inteqralları, indi keçəcəyəm. Hələ də belə bir inteqralla qarşılaşırsınızsa, dərsliyə baxın - orada hər şey sadədir. Düşünürəm ki, materialı (hətta sadə olanları) daxil etməyi məsləhət görmürəm, qarşılaşma ehtimalı sıfıra bərabərdir.

Mürəkkəb triqonometrik funksiyaların inteqrasiyası

Əksər nümunələr üçün “mürəkkəb” sifət yenə də əsasən şərtlidir. Yüksək güclərdəki tangens və kotangentlərdən başlayaq. İstifadə olunan həll üsulları nöqteyi-nəzərindən tangens və kotangens demək olar ki, eyni şeydir, ona görə də inteqralın həlli üçün nümayiş etdirilən metodun kotangens üçün də keçərli olduğunu bildirərək tangens haqqında daha çox danışacağam.

Yuxarıdakı dərsdə baxdıq universal triqonometrik əvəzetmə triqonometrik funksiyaların müəyyən növ inteqrallarının həlli üçün. Universal triqonometrik əvəzetmənin dezavantajı ondan ibarətdir ki, onun istifadəsi çox vaxt çətin hesablamalarla çətin inteqrallarla nəticələnir. Və bəzi hallarda universal triqonometrik əvəzlənmədən qaçınmaq olar!

Başqa bir kanonik nümunəyə, sinusla bölünən birinin inteqralına baxaq:

Misal 17

Qeyri-müəyyən inteqralı tapın

Burada universal triqonometrik əvəzetmədən istifadə edib cavab ala bilərsiniz, lakin daha rasional bir yol var. Hər addım üçün şərhlərlə tam həlli təqdim edəcəyəm:

(1) İkiqat bucağın sinusu üçün triqonometrik düsturdan istifadə edirik.
(2) Süni bir çevrilmə həyata keçiririk: Məxrəcə bölün və ilə vurun.
(3) Məxrəcdəki məlum düsturdan istifadə edərək kəsri tangensə çeviririk.
(4) Funksiyanı diferensial işarənin altına gətiririk.
(5) İnteqralı götürün.

Özünüz həll edə biləcəyiniz bir neçə sadə nümunə:

Misal 18

Qeyri-müəyyən inteqralı tapın

Qeyd: İlk addım azalma düsturundan istifadə etmək olmalıdır və əvvəlki nümunəyə bənzər hərəkətləri diqqətlə yerinə yetirin.

Misal 19

Qeyri-müəyyən inteqralı tapın

Yaxşı, bu çox sadə bir nümunədir.

Dərsin sonunda həllər və cavabları tamamlayın.

Düşünürəm ki, indi heç kimin inteqrallarla problemi olmayacaq:
və s.

Metodun ideyası nədir? İdeya çevrilmələrdən və triqonometrik düsturlardan istifadə edərək yalnız tangensləri və toxunan törəməni inteqrana çevirməkdir. Yəni, əvəz etməkdən danışırıq: . Nümunələr 17-19-da biz əslində bu əvəzetmədən istifadə etdik, lakin inteqrallar o qədər sadə idi ki, biz ekvivalent bir hərəkətlə - funksiyanı diferensial işarənin altında toplamaqla başa düşdük.

Oxşar mülahizə, artıq qeyd etdiyim kimi, kotangent üçün də aparıla bilər.

Yuxarıdakı əvəzin tətbiqi üçün rəsmi şərt də var:

Kosinusun və sinusun səlahiyyətlərinin cəmi mənfi tam ədəd CEVAP ədədidir, Misal üçün:

inteqral üçün – mənfi tam ədəd EVEN ədədi.

! Qeyd : əgər inteqral YALNIZ sinus və ya YALNIZ kosinusu ehtiva edirsə, onda inteqral da mənfi tək dərəcə üçün götürülür (ən sadə hallar 17, 18 Nömrələrdədir).

Bu qaydaya əsaslanaraq bir neçə daha mənalı işə baxaq:

Misal 20

Qeyri-müəyyən inteqralı tapın

Sinus və kosinusun səlahiyyətlərinin cəmi: 2 – 6 = –4 mənfi tam ədəd HƏFTƏ ədəddir, yəni inteqral tangenslərə və onun törəməsinə endirilə bilər:

(1) Məxrəci çevirək.
(2) Tanınmış düsturdan istifadə edərək, əldə edirik.
(3) Məxrəci çevirək.
(4) Düsturdan istifadə edirik .
(5) Funksiyanı diferensial işarənin altına gətiririk.
(6) Biz dəyişdirmə həyata keçiririk. Daha təcrübəli tələbələr dəyişdirməni həyata keçirməyə bilər, lakin yenə də tangensi bir hərflə əvəz etmək daha yaxşıdır - çaşqınlıq riski azdır.

Misal 21

Qeyri-müəyyən inteqralı tapın

Bu, özünüz həll etməyiniz üçün bir nümunədir.

Dayan, çempionat mərhələləri başlayır =)

Çox vaxt inteqralda "hodgepodge" var:

Misal 22

Qeyri-müəyyən inteqralı tapın

Bu inteqral əvvəlcə bir tangens ehtiva edir ki, bu da dərhal artıq tanış bir fikrə gətirib çıxarır:

Süni çevrilməni ən əvvəldə və qalan addımları şərhsiz tərk edəcəyəm, çünki hər şey yuxarıda müzakirə edilmişdir.

Öz həlliniz üçün bir neçə yaradıcı nümunə:

Misal 23

Qeyri-müəyyən inteqralı tapın

Misal 24

Qeyri-müəyyən inteqralı tapın

Bəli, onlarda, əlbəttə ki, sinus və kosinusun səlahiyyətlərini aşağı sala bilərsiniz və universal triqonometrik əvəzetmədən istifadə edə bilərsiniz, lakin tangentlər vasitəsilə həyata keçirilərsə, həll daha səmərəli və daha qısa olacaqdır. Tam həll və dərsin sonunda cavablar