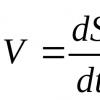Равноускоренное движение - это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение - частный случай равноускоренного движения с ускорением, равным нулю.

Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.

В любой точке траектории на тело действует ускорение свободного падения g → , которое не меняется по величине и всегда направлено в одну сторону.

Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y - равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.

Формула для скорости при равноускоренном движении:

Здесь v 0 - начальная скорость тела, a = c o n s t - ускорение.

Покажем на графике, что при равноускоренном движении зависимость v (t) имеет вид прямой линии.

​​​​​​​

Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.

a = v - v 0 t = B C A C

Чем больше угол β , тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v 0 = - 2 м с; a = 0 , 5 м с 2 .

Для второго графика: v 0 = 3 м с; a = - 1 3 м с 2 .

По данному графику можно также вычислить перемещение тела за время t . Как это сделать?

Выделим на графике малый отрезок времени ∆ t . Будем считать, что он настолько мал, что движение за время ∆ t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆ t . Тогда, перемещение ∆ s за время ∆ t будет равно ∆ s = v ∆ t .

Разобьем все время t на бесконечно малые промежутки ∆ t . Перемещение s за время t равно площади трапеции O D E F .

s = O D + E F 2 O F = v 0 + v 2 t = 2 v 0 + (v - v 0) 2 t .

Мы знаем, что v - v 0 = a t , поэтому окончательная формула для перемещения тела примет вид:

s = v 0 t + a t 2 2

Для того, чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты в зависимости от времени выражает закон равноускоренного движения.

Закон равноускоренного движения

y = y 0 + v 0 t + a t 2 2 .

Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения - нахождение координаты при заданных значениях начальной и конечной скоростей и ускорения.

Исключая из записанных выше уравнений t и решая их, получаем:

s = v 2 - v 0 2 2 a .

По известным начальной скорости, ускорению и перемещению можно найти конечную скорость тела:

v = v 0 2 + 2 a s .

При v 0 = 0 s = v 2 2 a и v = 2 a s

Важно!

Величины v , v 0 , a , y 0 , s , входящие в выражения, являются алгебраическими величинами. В зависимости от характера движения и направления координатных осей в условиях конкретной задачи они могут принимать как положительные, так и отрицательные значения.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

3.2.1. Как правильно понимать условия задачи?

Скорость тела увеличилась в n раз:

Скорость уменьшилась в n раз:

Скорость увеличилась на 2 м/с:

Во сколько раз увеличилась скорость?

Во сколько раз уменьшилась скорость?

Как изменилась скорость?

На сколько увеличилась скорость?

На сколько уменьшилась скорость?

Тело достигло наибольшей высоты:

Тело прошло половину расстояния:

Тело бросают с земли: (последнее условие часто ускользает из вида - если у тела скорость равна нулю, например у ручки, лежащей на столе, оно может полететь само вверх?), начальная скорость направлена вверх.

Тело бросают вниз: начальная скорость направлена вниз.

Тело бросают вверх: начальная скорость направлена вверх.

В момент падения на землю:

Тело выпадает из аэростата (воздушного шара): начальная скорость равна скорости аэростата (воздушного шара) и направлена в ту же самую сторону.

3.2.2. Как по графику скорости определить ускорение?

Закон изменения скорости имеет вид:

Графиком этого уравнения является прямая линия. Так как - коэффициент перед t , то является угловым коэффициентом прямой.

Для графика 1:

То, что график 1 «поднимается вверх», означает - проекция ускорения положительна, т. е. вектор направлен в положительном направлении оси Ox

Для графика 2:

То, что график 2 «опускается вниз», означает - проекция ускорения отрицательна, т. е. вектор направлен в отрицательном направлении оси Ox . Пересечение графика с осью - изменение направления движения на противоположное.

Для определения и выбираем такие точки на графике, в которых можно точно определить значения, как правило, это точки, находящиеся в вершинах клеток.

3.2.3. Как по графику скорости определить пройденный путь и перемещение?

Как сказано в пункте 3.1.6 путь можно как площадь под графиком зависимости скорости от ускорения. Простой случай показан в пункте 3.1.6. Рассмотрим более сложный вариант, когда график скорости пересекает ось времени.

Напомним, что путь может только увеличиваться, поэтому путь, который проехало тело в примере на рисунке 9 равен:

где и - площади фигур, закрашенных на рисунке.

Для определения перемещения нужно заметить, что в точках и тело меняет направление движения. Проезжая путь тело движется в положительном направлении оси Ox , так как график лежит над осью времени. Проезжая путь тело движется в обратную сторону, в отрицательном направлении оси Ox так как график лежит под осью времени. Проезжая путь , тело движется в положительном направлении оси Ox , так как график лежит над осью времени. Таким образом, перемещение равно:

Еще раз обратим внимание:

1) пересечение с осью времени означает поворот в обратную сторону;

2) площадь графика, лежащего под осью времени положительна и входит со знаком «+» в определение пройденного пути, но со знаком «−» в определении перемещения.

3.2.4. Как из графика зависимости ускорения от времени определить зависимость скорости от времени и координаты от времени?

Для того, чтобы определить требуемые зависимости необходимы начальные условия - значения скорости и координаты в момент времени Без начальных условий решить однозначно данную задачу невозможно, поэтому, как правило, в условии задачи они даны.

В данном примере постараемся привести все рассуждения в буквах, для того, чтобы частном примере (при подстановке цифр) не потерять суть действий.

Пусть в момент времени скорость тела равна нулю и начальная координата

Начальные значения скорости и координаты определяем из начальных условий, а ускорение из графика:

следовательно, движение равноускоренное и закон изменения скорости имеет вид:

К концу данного промежутка времени () скорость () и координата () будут равны (вместо времени в формулы и нужно подставить ):

Начальное значение скорости на этом промежутке должно быть равно конечному значению на предыдущем промежутке, начальное значение координаты равно конечному значению координаты на предыдущем промежутке, а ускорение определяем из графика:

следовательно, движение равноускоренное и закон изменения скорости имеет вид:

К концу данного промежутка времени () скорость () и координата () будут равны (вместо времени в формулы и нужно подставить ):

Для лучшего понимания построим полученные результаты на графике (см. рис.)

На графике скорости:

1) От 0 до прямая линия, «поднимающаяся вверх» (т. к. );

2) От до горизонтальная прямая линия (т. к. );

3) От до : прямая линия, «опускающаяся вниз» (т. к. ).

На графике координаты:

1) От 0 до : парабола, ветви которой направлены вверх (т. к. );

2) От до : прямая линия, поднимающаяся вверх (т. к. );

3) От до : парабола, ветви которой направлены вниз (т. к. ).

3.2.5. Как из графика закона движения записать аналитическую формулу закона движения?

Пусть дан график равнопеременного движения.

В этой формуле три неизвестные величины: и

Для определения достаточно посмотреть на значение функции при Для определения двух других неизвестных выбираем две точки на графике, значения которых мы можем точно определить - вершины клеток. Получим систему:

При этом считаем, что нам уже известно. Умножим 1-ое уравнение системы на а 2-ое уравнение на :

Вычтем из 1-го уравнения 2-ое, после чего получаем:

Полученное из данного выражения значение подставим в любое из уравнений системы (3.67) и решим полученное уравнение относительно :

3.2.6. Как по известному закону движения определить закон изменения скорости?

Закон равнопеременного движения имеет вид:

Это его стандартный вид для данного типа движения и никак иначе он выглядеть не может, поэтому его стоит запомнить.

В данном законе коэффициент перед t - это значение начальной скорости, коэффициент пред - это ускорение, деленное пополам.

Например, пусть дан закон:

И уравнение скорости имеет вид:

Таким образом, для решения подобных задач, необходимо точно помнить вид закона равнопеременного движения и смысл коэффициентов, входящих в это уравнение.

Однако можно пойти и иным путем. Вспомним формулу:

В нашем примере:

3.2.7. Как определить место и время встречи?

Пусть даны законы движения двух тел:

В момент встречи тела оказываются в одной координате, то есть и необходимо решить уравнение:

Перепишем его в виде:

Это квадратное уравнение, общее решение которого приводить не будем, в силу его громоздкости. Квадратное уравнение либо не имеет решений, что означает - тела не встретились; либо имеет одно решение - одна единственная встреча; либо имеет два решения - две встречи тел.

Полученные решения необходимо проверять на физическую реализуемость. Самое главное условие: и то есть время встречи должно быть положительным.

3.2.8. Как определить путь за -ую секунду?

Пусть тело начинает движение из состояния покоя и за -ую секунду проходит путь Требуется найти, какой путь проходит тело за n -ую секунду.

Для решения этой задачи необходимо воспользоваться формулой (3.25):

Обозначим Тогда

Поделим уравнение на и получим:

3.2.9. Как движется тело, брошенное вверх с высоты h ?

Тело, брошено вверх с высоты h со скоростью

Уравнение координаты y

Время подъема до наивысшей точки полета определяется из условия :

H необходимо в необходимо подставить :

Скорость в момент падения:

3.2.10. Как движется тело, брошенное вниз с высоты h ?

Тело, брошено вверх с высоты h со скоростью

Уравнение координаты y в произвольный момент времени:

Уравнение :

Время всего полета определяется из уравнения:

Это квадратное уравнение, которое имеет два решения, но в данной задаче тело может оказаться в координате только один раз. Поэтому среди полученных решений нужно одно «убрать». Главный критерий отсева - время полета не может быть отрицательным:

Скорость в момент падения:

3.2.11. Как движется тело брошенное вверх с поверхности земли?

Тело брошено вверх с поверхности земли со скоростью

Уравнение координаты y в произвольный момент времени:

Уравнение проекции скорости в произвольный момент времени:

Время подъема до наивысшей точки полета определяется из условия

Для нахождения максимальной высоты H необходимо в (3.89) необходимо подставить

Время всего полета определяется из условия Получаем уравнение:

Скорость в момент падения:

Заметьте, что что означает - время подъема равно времени падения на ту же высоту.

Также получили: то есть - с какой скоростью бросили, с такой же скоростью тело упало. Знак «−» в формуле указывает, что скорость в момент падения направлена вниз, то есть против оси Oy .

3.2.12. Тело побывало на одной высоте дважды…

При бросании тела оно может дважды оказаться на одной высоте - первый раз при движении вверх, второй - при падении вниз.

1) Когда тело оказывается на высоте h ?

Для тела, брошенного вверх с поверхности земли справедлив закон движения:

Когда тело окажется на высоте h его координата будет равна Получаем уравнение:

решение которого имеет вид:

2) Известны времена и когда тело оказалось на высоте h . Когда тело окажется на максимальной высоте?

Время полета с высоты h назад до высоты h равно Как уже было показано, время подъема равно времени падения до той же высоты, поэтому время полета от высоты h до максимальной высоты равно:

Тогда время полета от начала движения до максимальной высоты:

3) Известны времена и когда тело оказалось на высоте h . Чему равно время полета тела?

Все время полета равно:

4) Известны времена и когда тело оказалось на высоте h . Чему равна максимальная высота подъема?

3.2.13. Как движется тело, брошенное горизонтально с высоты h ?

Тело, брошено горизонтально с высоты h со скоростью

Проекции ускорения:

Проекции скорости в произвольный момент времени t :

t :

t :

Время полета определяется из условия

Для определения дальности полета необходимо в уравнение для координаты x вместо t подставить

Для определения скорости тела в момент падения необходимо в уравнение вместо t подставить

Угол, под которым падает тело на землю:

3.2.14. Как движется тело, брошенное под углом α к горизонту с высоты h ?

Тело, брошено под углом α к горизонту с высоты h со скоростью

Проекции начальной скорости на оси:

Проекции ускорения:

Проекции скорости в произвольный момент времени t :

Модуль скорости в произвольный момент времени t :

Координаты тела в произвольный момент времени t :

Максимальная высота H

Это квадратное уравнение, которое имеет два решения, но в данной задаче тело может оказаться в координате только один раз. Поэтому среди полученных решений нужно одно «убрать». Главный критерий отсева - время полета не может быть отрицательным:

x L :

Скорость в момент падения

Угол падения:

3.2.15. Как движется тело, брошенное под углом α к горизонту земли?

Тело, брошено под углом α к горизонту с поверхности земли со скоростью

Проекции начальной скорости на оси:

Проекции ускорения:

Проекции скорости в произвольный момент времени t :

Модуль скорости в произвольный момент времени t :

Координаты тела в произвольный момент времени t :

Время полета до наивысшей точки определяется из условия

Скорость в наивысшей точке полета

Максимальная высота H определяется при подстановке в закон изменения координаты y времени

Все время полета находится из условия получаем уравнение:

Получаем

Снова получили, что то есть еще раз показали, что время подъема равно времени падения.

Если подставим в закон изменения координаты x время то получим дальность полета L :

Скорость в момент падения

Угол, который образует вектор скорости с горизонталью в произвольный момент времени:

Угол падения:

3.2.16. Что такое настильная и навесная траектории?

Решим следующую задачу: под каким углом нужно бросить тело с поверхности земли, чтобы тело упало на расстоянии L от точки броска?

Дальность полета определяется формулой:

Из физических соображений ясно, что угол α не может быть больше 90°, поэтому, из серии решений уравнения подходят два корня:

Траектория движения, для которой называется настильной траекторией. Траектория движения, для которой называется навесной траекторией.

3.2.17. Как пользоваться треугольником скоростей?

Как было сказано в 3.6.1 треугольник скоростей в каждой задаче будет иметь свой вид. Рассмотрим на конкретном примере.

Тело бросили с вершины башни со скорость так, что дальность полета максимальна. К моменту падения на землю скорость тела равна Сколько длился полет?

Построим треугольник скоростей (см. рис.). Проведем в ней высоту, которая, очевидно, равна Тогда площадь треугольника скоростей равна:

Здесь мы воспользовались формулой (3.121).

Найдем площадь этого же треугольника по другой формуле:

Так как это площади одного и того же треугольника, то приравняем формулы и :

Откуда получаем

Как видно из формул для конечной скорости, полученных в предыдущих пунктах, конечная скорость не зависит от угла, под которым бросили тело, а зависит только значения начальной скорости и начальной высоты. Поэтому дальность полета по формуле зависит только от угла между начальной и конечной скоростью β. Тогда дальность полета L будет максимальной, если примет максимально возможное значение, то есть

Таким образом, если дальность полета максимальна, то треугольник скоростей будет прямоугольным, следовательно, выполняется теорема Пифагора:

Откуда получаем

Свойством треугольника скоростей, который только что был доказан, можно пользоваться при решении других задач: треугольник скоростей является прямоугольным в задаче на максимальную дальность полета.

3.2.18. Как пользоваться треугольником перемещений?

Как было сказано в 3.6.2, треугольник перемещений в каждой задаче будет иметь свой вид. Рассмотрим на конкретном примере.

Тело бросают под углом β к поверхности горы, имеющей угол наклона α. С какой скоростью нужно бросить тело, чтобы оно упало ровно на расстоянии L от точки бросания?

Построим треугольник перемещений - это треугольник ABC (см. рис. 19). Проведем в нем высоту BD . Очевидно, что угол DBC равен α.

Выразим сторону BD из треугольника BCD :

Выразим сторону BD из треугольника ABD :

Приравняем и :

Откуда находим время полета:

Выразим AD из треугольника ABD :

Выразим сторону DC из треугольника BCD :

Но Получаем

Подставим в это уравнение, полученное выражение для времени полета :

Окончательно получаем

3.2.19. Как решать задачи с помощью закона движения? (по горизонтали)

Как правило, в школе при решении задач на равнопеременное движение применяются формулы

Однако такой подход к решению трудно применить к решению многих задач. Рассмотрим конкретный пример.

Опоздавший пассажир подошёл к последнему вагону поезда в тот момент, когда поезд тронулся, начав движение с постоянным ускорением Единственная открытая дверь в одном из вагонов оказалась от пассажира на расстоянии Какую наименьшую постоянную скорость он должен развить, чтобы успеть сесть в поезд?

Введем ось Ox , направленную вдоль движения человека и поезда. За нулевое положение примем начальное положение человека («2»). Тогда начальная координата открытой двери («1») L :

Дверь («1»), как и весь поезд, имеют начальную скорость равную нулю. Человек («2») начинает движение со скоростью

Дверь («1»), как и весь поезд, движется с ускорением a. Человек («2») движется с постоянной скоростью:

Закон движения и двери и человека имеет вид:

Подставим условия и в уравнение для каждого из движущихся тел:

Мы составили уравнение движения для каждого из тел. Теперь воспользуемся уже известным алгоритмом для нахождения места и времени встречи двух тел - нам нужно приравнять и :

Откуда получаем квадратное уравнение для определения времени встречи:

Это квадратное уравнение. Оба его решения имеют физический смысл - наименьший корень, это первая встреча человека и двери (человек с места может побежать быстро, а поезд не сразу наберет большую скорость, так что человек может обогнать дверь), второй корень - вторая встреча (когда уже поезд разогнался и догнал человека). Но наличие обоих корней означает - человек может бежать и медленнее. Скорость будет минимальна, когда уравнение будет иметь один единственный корень, то есть

Откуда находим минимальную скорость:

В таких задачах важно разобрать в условиях задачи: чему равны начальная координата, начальная скорость и ускорение. После этого составляем уравнение движения и думаем как дальше решать задачу. 

3.2.20. Как решать задачи с помощью закона движения? (по вертикали)

Рассмотрим пример.

Свободно падающее тело прошло последние 10 м за 0,5 с. Найти время падения и высоту, с которой упало тело. Сопротивлением воздуха пренебречь.

Для свободного падения тела справедлив закон движения:

В нашем случае:

начальная координата:

начальная скорость:

Подставим условия в закон движения:

Подставляя в уравнение движения нужные значения времени, будем получать координаты тела в эти моменты.

В момент падения координата тела

За с до момента падения, то есть при координата тела

Уравнения и составляют систему уравнений, в которой неизвестны H и Решая эту систему, получим:

Итак, зная вид закона движения (3.30), и используя условия задачи для нахождения и получаем закон движения для данной конкретной задачи. После чего, подставляя нужные значения времени, получаем соответствующие значения координаты. И решаем задачу!

На данном уроке мы с вами рассмотрим важную характеристику неравномерного движения - ускорение. Кроме того, мы рассмотрим неравномерное движение с постоянным ускорением. Такое движение еще называется равноускоренным или равнозамедленным. Наконец, мы поговорим о том, как графически изображать зависимости скорости тела от времени при равноускоренном движении.

Домашнее задание

Решив задачи к данному уроку, вы сможете подготовиться к вопросам 1 ГИА и вопросам А1, А2 ЕГЭ.

1. Задачи 48, 50, 52, 54 сб. задач А.П. Рымкевич, изд. 10.

2. Запишите зависимости скорости от времени и нарисуйте графики зависимости скорости тела от времени для случаев, изображенных на рис. 1, случаи б) и г). Отметьте на графиках точки поворота, если такие есть.

3. Рассмотрите следующие вопросы и ответы на них:

Вопрос. Является ли ускорение свободного падения ускорением, согласно данному выше определению?

Ответ. Конечно, является. Ускорение свободного падения - это ускорение тела, которое свободно падает с некоторой высоты (сопротивлением воздуха нужно пренебречь).

Вопрос. Что произойдет, если ускорение тела будет направлено перпендикулярно скорости движения тела?

Ответ. Тело будет двигаться равномерно по окружности.

Вопрос. Можно ли вычислять тангенс угла наклона, воспользовавшись транспортиром и калькулятором?

Ответ. Нет! Потому что полученное таким образом ускорение будет безразмерным, а размерность ускорения, как мы показали ранее, должно иметь размерность м/с 2 .

Вопрос. Что можно сказать о движении, если график зависимости скорости от времени не является прямой?

Ответ. Можно сказать, что ускорение этого тела меняется со временем. Такое движение не будет являться равноускоренным.

Рассмотрим движение тела, брошенного горизонтально и движущегося под действием одной только силы тяжести (сопротивлением воздуха пренебрегаем). Например, представим себе, что шару, лежащему на столе, сообщают толчок, и он докатывается до края стола и начинает свободно падать, имея начальную скорость , направленную горизонтально (рис. 174).

Спроектируем движение шара на вертикальную ось и на горизонтальную ось . Движение проекции шара на ось - это движение без ускорения со скоростью ; движение проекции шара на ось - это свободное падение с ускорением бее начальной скорости под действием силы тяжести. Законы обоих движений нам известны. Компонента скорости остается постоянной и равной . Компонента растет пропорционально времени: . Результирующую скорость легко найти по правилу параллелограмма, как показано на рис. 175. Она будет наклонена вниз, и ее наклон будет расти с течением времени.

Рис. 174. Движение шара, скатившегося со стола

Рис. 175. Шар, брошенный горизонтально со скоростью имеет в момент скорость

Найдем траекторию тела, брошенного горизонтально. Координаты тела в момент времени имеют значения

Чтобы найти уравнение траектории, выразим из (112.1) время через и подставим это выражение в (112.2). В результатё получим

График этой функции показан на рис. 176. Ординаты точек траектории оказываются пропорциональными квадратам абсцисс. Мы знаем, что такие кривые называются параболами. Параболой изображался график пути равноускоренного движения (§ 22). Таким образом, свободно падающее тело, начальная скорость которого горизонтальна, движется по параболе.

Путь, проходимый в вертикальном направлении, не зависит от начальной скорости. Но путь, проходимый в горизонтальном направлении пропорционален начальной скорости. Поэтому при большой горизонтальной начальной скорости парабола, по которой падает тело, более вытянута в горизонтальном направлении. Если из расположенной горизонтально трубки выпускать струю воды (рис. 177), то отдельные частицы воды будут, так же как и шарик, двигаться по параболе. Чем больше открыт кран, через который поступает вода в трубку, тем больше начальная скорость воды и тем дальше от крана попадает струя на дно кюветы. Поставив позади струи экран с заранее начерченными на нем параболами, можно убедиться, что струя воды действительно имеет форму параболы.