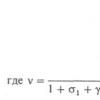Какая математическая модель не относится к стохастическим. Стохастическая модель процесса. Классификация средств моделирования
Стохастический вариант даже простой эпидемии достаточно сложен. Не удивительно, что в общем случае для анализа стохастической модели эпидемии требуется еще более сложный математический аппарат. По-настоящему удовлетворительное описание основных характеристик такого процесса еще не достигнуто, но ряд отдельных полезных результатов уже получен.
Рассмотрим вначале исходную модель и вывод основных уравнений движения. В данном случае имеются две существенно различные случайные величины. Пусть, как и ранее, обозначает число восприимчивых индивидуумов в момент времени t, a - число источников инфекции. Таким образом, мы имеем дело с двумерным процессом, аналогичным тому, который был рассмотрен в разд. 8.3. Здесь возможны переходы двух видов. Снова примем частоту контактов равной тогда вероятность появления в интервале нового источника инфекции будет равна . Если частота удаления из коллектива зараженных индивидуумов равна у, то вероятность того, что в интервале будет удален один индивидуум, составит . В данном случае возможны два значения функции отличные от нуля; в обозначениях, принятых в разд. 8.2 и 8.3, они имеют вид . Если изменить временной масштаб, перейдя к и обозначить через относительную частоту удаления, то, используя уравнение (8.48), получим следующее дифференциальное уравнение в частных производных для производящей функции вероятностей:
при начальном условии
(в предположении, что процесс начинается при наличии восприимчивых индивидуумов и а источников инфекции).
До сих пор непосредственно решить уравнение (9.24) в простом замкнутом виде еще не удалось. Попытки использовать обыкновенные дифференциальные уравнения для моментов или семиинвариантов, выведенные обычным способом, также не увенчались успехом по тем же причинам, что и в случае модели конкуренции между двумя видами, рассмотренной в разд. 8.4. (Такая же трудность возникает даже в случае простой стохастической эпидемии.) Однако не исключено, что уравнение (9.24) можно будет использовать как основу для дальнейших исследований.
Если вероятность того, что в момент имеется j восприимчивых индивидуумов и к источников инфекции, равна , то подстановка производящей функции вероятностей
![]()
в уравнение (9.24) дает систему дифференциальных уравнений

В принципе эти уравнения можно решить непосредственно с помощью преобразований Лапласа. Однако получающиеся алгебраические выражения столь громоздки, что практически этот метод совершенно непригоден.
Некоторого успеха можно добиться в предельном случае при когда . Здесь можно получить довольно простую треугольную систему линейных уравнений, решение которой дает вероятность того, что дополнительно к первоначальным случаям эпидемия охватит еще w индивидуумов. Для получения конкретных результатов необходимо провести численные расчеты; были рассчитаны распределения общего числа зараженных индивидуумов для и 40 при и различных значениях . Как и ожидалось, при все распределения имеют -образную форму с максимальным значением в точке Если же , то распределения имеют -образную форму, т. е. возможна очень малая или очень большая вспышка, тогда как промежуточные состояния наблюдаются редко.
Таким образом, хотя при столь малых значениях (не более 40) резкие переходы отсутствуют, имеются две различные схемы распространения эпидемии.
При больших справедлива теорема о стохастическом пороговом значении, принадлежащая Уиттлу. Не входя во все детали анализа, проведенного Уиттлом, с помощью следующих приближенных рассуждений легко показать, чего именно можно ожидать в этом случае. Если достаточно велико, то (во всяком случае, в начальный период) численность группы источников инфекции изменяется примерно по тому же закону, которому подчиняется процесс размножения и гибели со скоростями размножения и гибели, равными соответственно и у. Теперь используем формулу (8.35), выражающую вероятность вымирания популяции, заменив , на на у. Из нее следует, что вероятность прекращения эпидемического процесса равна 1 при и при . В первом случае исходная группа источников инфекции, безусловно, элиминирует и можно ожидать, что общее число заболеваний будет мало. Во втором случае с вероятностью можно ожидать малой вспышки и с вероятностью - большой вспышки эпидемии.
Стохастические модели с такими общими свойствами весьма полезны, хотя и до известного предела. Несмотря на присущие им ограничения, эти модели, соответствующим образом обобщенные и измененные, смогут, по-видимому, сыграть важную роль при исследовании широкого круга эпидемических явлений, наблюдаемых в больших популяциях. Однако очевидно, что для изучения более тонких деталей эти модели не подойдут. Так, в рассмотренной выше стохастической модели предполагалось, что не только латентный период равен нулю, но и длительность заразного периода имеет экспоненциальное распределение; для большинства болезней ни одно из этих допущений не справедливо. Для более реалистичного описания биологических и клинических деталей можно было бы построить модели для многофазовых процессов аналогично тому, что было сделано в конце разд. 8.3. Затем для различных интервалов можно выбрать распределения сохраняя при этом марковский характер всего процесса. В определенных случаях оказываются применимыми модели, рассмотренные в разд. 9.5 и 9.6.

Математические схемы описания технических систем
Общая классификация моделей систем
Все то на что направлена человеческая деятельность называется объектом . Определяя роль теории моделирования в процессе изучения объектов, а значит их моделей, необходимо отвлечься от их разнообразия и выделить общее, что присуще моделям различных по своей природе объектов. Этот подход привел к появлению общей классификации моделей систем.
Создаваемые модели систем классифицируются:
· по времени
* динамические модели: непрерывные, которые описываются дифференциальными уравнениями; дискретно–непрерывные (разностные), описываются разностными уравнениями; вероятностные, построенные на событиях – модели теории массового обслуживания;
* дискретные модели – автоматы;
· по признаку случайности :
* детерминированные – модели отражающие процессы, в которых отсутствуют всякие случайные воздействия;
* стохастические – модели отражающие вероятностные процессы и события;
· по назначению :
· по виду обрабатываемой информации :
* информационные: - справочно-информационные;
Информационно -советующие;
Экспертные;
Автоматические;
* физические модели: - натурные (плазма);
Полунатурные (аэродинамические трубы);
* имитационные модели;
* интеллектуальные модели;
* семантические (логические) модели;
Перейдем к рассмотрению основных видов математических схем .
1.3.1. Непрерывно–детерминированные модели (D – схемы)
Математические схемы такого вида отражают динамику процессов, протекающих во времени в системе. Поэтому они называются D– схемы. Частным случаем динамических систем являются системы автоматического управления .
Линейная автоматическая система описывается линейным дифференциальным уравнением вида
где x(t) - задающее воздействие или входная переменная системы; y(t) - состояние системы или выходная переменная; - коэффициенты; t - время.
На рис.1 представлена укрупненная функциональная схема системы автоматического управления, где – сигнал ошибки; - управляющее воздействие; f(t) - возмущающее воздействие. Данная система основана на принципе отрицательной обратной связи, так как для приведения выходной переменной y(t) к ее заданному значению используется информация об отклонении между ними. По ней можно разработать структурную схему и математическую модель в виде передаточной функции или в виде дифференциального уравнения (1.1), в котором для простоты предполагается, что точки приложения возмущающих воздействий совпадают с входом системы.
Рис.1.1. Структура системы автоматического управления
Непрерывно- детерминированные схемы (D- схемы) выполняются на аналоговых вычислительных машинах (АВМ).
1.3.2. Дискретно–детерминированные модели (F – схемы)
Основным видом дискретно–детерминированных моделей является конечный автомат.
Конечным автоматом называют дискретный преобразователь информации, способный под воздействием входных сигналов переходить из одного состояния в другое и формировать сигналы на выходе. Это автомат с памятью . Для организации памяти в описание автомата вводят автоматное время и понятие состояние автомата .
Понятие «состояние» автоматаозначает, что выходной сигнал автомата зависит не только от входных сигналов в данный момент времени, но и учитывает входные сигналы, поступающие ранее. Это позволяет устранить время как явную переменную и выразить выходные сигналы как функцию состояний и входных сигналов.
Всякий переход автомата из одного состояния в другое возможен не ранее, чем через дискретный интервал времени. Причем сам переход считается, происходит мгновенно, то есть не учитывают переходные процессы в реальных схемах.
Существует два способа введения автоматного времени по которому автоматы делятся на синхронные и асинхронные .
В синхронных автоматах моменты времени, в которых фиксируются изменения состояний автомата, задаются специальным устройством – генератором синхросигналов. Причем сигналы поступают через равные интервалы времени – . Частота тактового генератора выбирается такой, чтобы любой элемент автомата успел закончить свою работу до появления очередного импульса.
В асинхронном автомате моменты перехода автомата из одного состояния в другое заранее не определены и зависят от конкретных событий. В таких автоматах интервал дискретности является переменным.
Также существуют детерминированные и вероятностные автоматы.
В детерминированных автоматах поведение и структура автомата в каждый момент времени однозначно определены текущей входной информацией и состоянием автомата.
В вероятностных автоматах они зависят от случайного выбора.
Абстрактно конечный автомат можно представить как математическую схему (F – схему), которая характеризуется шестью видами переменных и функций:
1) конечное множество x(t) входных сигналов (входной алфавит);
2) конечное множество y(t) выходных сигналов (выходной алфавит);
3) конечное множество z(t) внутренних состояний (алфавит состояний);
4) начальное состояние автомата z 0 , ;
5) функция переходов автомата из одного состояния в другое;
6) функция выходов автомата.
Абстрактный конечный автоматимеет один вход и один выход. В каждый дискретный момент времени t=0,1,2,... F– автомат находится в определенном состоянии z(t) из множества Z – состояний автомата, причем в начальный момент времени t=0 он всегда находится в начальном состоянии z(0)=z 0 . В момент t , будучи в состоянии z(t) , автомат способен воспринять на входном канале сигнал и выдать на выходном канале сигнал , переходя в состояние
Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита X на множество слов выходного алфавита Y , то есть, если на вход конечного автомата, установленного в начальное состояние z 0 , подавать в некоторой последовательности буквы входного алфавита , которые составляют входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита образуя выходное слово.
Следовательно, работа конечного автомата происходит по следующей схеме: на каждом t – ом такте на вход автомата, находящегося в состоянии z(t) , подается некоторый сигнал x(t) , на который автомат реагирует переходом на (t+1)– ом такте в новое состояние z(t+1) и выдачей некоторого выходного сигнала.
В зависимости от способа определения выходного сигнала синхронные абстрактные конечные автоматы подразделяются на два типа:
F – автомат первого рода, также называется автомат Мили :
F – автомат второго рода:
Автомат второго рода, для которого
называется автомат Мура – функция выходов не зависит от входной переменной x(t) .
Чтобы задать конечный F – автомат, необходимо описать все элементы множества .
Существует несколько способов задания работы F – автоматов среди которых наибольшее применение нашли табличный, графический и матричный.
1.3.3. Дискретно – непрерывные модели
Процессы в линейных импульсных и цифровых системах автоматического управления описываются дискретно – разностными уравнениями вида:
где x(n) –решетчатая функция входного сигнала; y(n) –решетчатая функция выходного сигнала, которая определяется решением уравнения (1.2); b k – постоянные коэффициенты; – разность к – го порядка; t=nT , где nT – n– ый момент времени, T – период дискретности (в выражении (1.2) он условно принят за единицу).
Уравнение (1.2) можно представить в другом виде:
Уравнение (1.3) представляет собой рекуррентное соотношение, которое позволяет вычислить любой (i+1) –й член последовательности по значениям предыдущих её членов i,i-1,... и значению x(i+1).
Основным математическим аппаратом моделирования цифровых автоматических систем является Z– преобразование, которое базируется на дискретном преобразовании Лапласа. Для этого необходимо найти импульсную передаточную функцию системы, задаться входной переменной и, варьируя параметрами системы, можно найти лучший вариант проектируемой системы.
1.3.4. Дискретно – стохастические модели (Р - схемы)
К дискретно – стохастической модели относится вероятностный автомат . В общем, виде вероятностный автомат является дискретным потактным преобразователем информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически. Поведение автомата зависит от случайного выбора.
Применение схем вероятностных автоматов имеет важное значение для проектирования дискретных систем, в которых проявляется статистически закономерное случайное поведение.
Для Р – автомата вводится аналогичное математическое понятие, как и для F – автомата. Рассмотрим множество G, элементами которого являются всевозможные пары (x i ,z s) , где x i и z s элементы входного подмножества X и подмножества состояний Z соответственно. Если существуют две такие функции и , что с их помощью осуществляется отображение и , то говорят, что определяет автомат детерминированного типа.
Функция переходов вероятностного автомата определяет не одно конкретное состояние, а распределение вероятностей на множестве состояний
(автомат со случайными переходами). Функция выходов также есть распределение вероятностей на множестве выходных сигналов (автомат со случайными выходами).
Для описания вероятностного автомата введем в рассмотрение более общую математическую схему. Пусть Ф – множество всевозможных пар вида (z k ,y j) , где y j – элемент выходного подмножества Y . Далее потребуем чтобы любой элемент множества G индуцировал на множестве Ф некоторый закон распределения следующего вида:
элементы из Ф...
где – вероятности перехода автомата в состояние z k и появления на выходе сигнала y j , если он был в состоянии z s и на его вход в этот момент времени поступал сигнал x i .
Число таких распределений, представленных в виде таблиц равно числу элементов множества G. Если обозначить это множество таблиц через В, то тогда четверку элементов называют вероятностным автоматом (Р – автоматом). При этом .
Частным случаем Р– автомата, задаваемого как являются автоматы, у которых либо переход в новое состояние, либо выходной сигнал определяются детерминировано(Z– детерминированный вероятностный автомат, Y–- детерминированный вероятностный автомат соответственно).
Очевидно, что с точки зрения математического аппарата задание Y – детерминированного Р – автомата эквивалентно заданию некоторой марковской цепи с конечным множеством состояний. В связи с этим аппарат марковских цепей является основным при использовании Р– схем для аналитических расчетов. Подобные Р– автоматы используют генераторы марковских последовательностей при построении процессов функционирования систем или воздействий внешней среды.
Марковские последовательности , согласно теореме Маркова, –это последовательность случайных величин, для которой справедливо выражение
где N – количество независимых испытаний; D–- дисперсия.
Такие Р– автоматы (Р– схемы) могут быть использованы для оценки различных характеристик исследуемых систем как для аналитических моделей, так и для имитационных моделей с использованием методов статистического моделирования.
Y – детерминированный Р– автомат можно задать двумя таблицами: переходов (табл.1.1) и выходов (табл.1.2).
Таблица 1.1
Где P ij – вероятность перехода Р– автомата из состояния z i в состояние z j , при этом .
Таблицу 1.1 можно представить в виде квадратной матрицы размерности . Такую таблицу будем называть матрицей переходных вероятностей или просто матрицей переходов Р- автомата , которую можно представить в компактной форме:
Для описания Y– детерминированного Р–автомата необходимо задать начальное распределение вероятностей вида:
| Z... | z 1 | z 2 | ... | z k-1 | z k |
| D... | d 1 | d 2 | ... | d k-1 | d k |
где d k– вероятность того, что в начале работы Р– автомат находится в состоянии z k , при этом .
И так, до начала работы Р– автомат находится в состоянии z 0 и в начальный (нулевой) такт времени меняет состояние в соответствии с распределением D. После этого смена состояний автомата определяется матрицей переходов Р. С учетом z 0 размерность матрицы Р р следует увеличить до , при этом первая строка матрицы будет (d 0 ,d 1 ,d 2 ,...,d k) , а первый столбец будет нулевым.
Пример. Y– детерминированный Р– автомат задан таблицей переходов:
Таблица 1.3
и таблицей выходов
Таблица 1.4
| Z | z 0 | z 1 | z 2 | z 3 | z 4 |
| Y |
С учетом таблицы 1.3 граф переходов вероятностного автомата представлен на рис.1.2.
Требуется оценить суммарные финальные вероятности пребывания этого автомата в состоянии z 2 и z 3 , т.е. когда на выходе автомата появляются единицы.
Рис. 1.2. Граф переходов
При аналитическом подходе можно использовать известные соотношения из теории марковских цепей и получить систему уравнений для определения финальных вероятностей. Причем начальное состояние можно не учитывать в виду того, что начальное распределение не оказывает влияние на значения финальных вероятностей. Тогда таблица 1.3 примет вид:
где – финальная вероятность пребывания Y– детерминированного Р– автомата в состоянии z k .
В результате получаем систему уравнений:
К данной системе следует добавить условие нормировки:
Теперь решая систему уравнений (1.4) совместно с (1.5), получаем:
Таким образом, при бесконечной работе заданного автомата на его выходе будет формироваться двоичная последовательность с вероятностью появления единицы, равной: .
Кроме аналитических моделей в виде Р– схем можно применять и имитационные модели, реализуемые, например, методом статистического моделирования.
1.3.5. Непрерывно–стохастические модели (Q– схемы)
Такие модели рассмотрим на примере использования в качестве типовых математических схем систем массового обслуживания, которые называют Q– схемами . Такие Q– схемы применяются при формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания .
К процессам обслуживания можно отнести: потоки поставок продукции некоторому предприятию, потоки деталей и комплектующих изделий на сборочном конвейере цеха, заявки на обработку информации ЭВМ от удаленных терминалов сети ЭВМ. Характерным признаком для функционирования таких систем или сетей является случайное появление заявок на обслуживание. Причем в любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания и, собственно, сам процесс обслуживания заявки. Представим это в виде некоторого i-го прибора обслуживания П i (рис.1.3), состоящего из накопителя заявок Н i , в котором может находится одновременно заявок; К i – канал обслуживания заявок.
На каждый элемент прибора П i поступают потоки событий, в накопитель Н i поток заявок , на канал К i – поток обслуживания И i .
Рис.1.3. Прибор обслуживания
Потоки событий могут быть однородными , если он характеризуется только последовательностью поступления этих событий (), или неоднородными , если он характеризуется набором признаков события, например таким набором признаков: источник заявок, наличие приоритета, возможность обслуживания тем или иным типом канала и т.п.
Обычно при моделировании различных систем применительно к каналу К i можно считать, что поток заявок на входе К i образует подмножество неуправляемых переменных, а поток обслуживания И i – образует подмножество управляемых переменных.
Те заявки, которые по различным причинам не обслуживаются каналом К i , образуют выходной поток У i .
Эти модели можно отнести к оптимальным стохастическим моделям.
Во многих случаях при построении модели не все условия заранее известны. Эффективность нахождения модели здесь будет зависеть от трех факторов:
Заданных условий х 1 , x 2 ,...,x n ;
Неизвестных условий y 1 ,y 2 ,...,y k ;
Зависящих от нас факторов и 1 ,и 2 ,...,и m , которые необходимо найти.
Показатель эффективности решения такой задачи имеет вид:
Наличие неизвестных факторов y i переводит задачу оптимизации в задачу о выборе решения в условиях неопределенности. Задача становится чрезвычайно сложной.
Особенно задача осложняется для случаев, когда величины y i не обладают статистической устойчивостью, то есть неизвестные факторы y i нельзя изучить с помощью статистических методов. Их законы распределения либо не могут быть получены, либо вовсе не существуют.
В этих случаях рассматриваются комбинации всевозможных значений Y:таким образом, чтобы получить как «наилучшее», так и «наихудшее» сочетания значений переменных y i .
Тогда в качестве критерия оптимизации рассматривается.
7.1 Сущность и задачи стохастического моделирования
Задачи детерминированного факторного анализа (ДФА) нашли широкое применение в практике аналитической работы, однако детерминированный подход не позволяет учитывать влияние на результативный показатель очень многих факторов, не находящихся с ним в пропорциональной зависимости (спрос, текучесть кадров, размещение торговой сети и т. д.). Кроме того, в задачах ДФА невозможно выделить результаты одновременно действующих факторов. Эти недостатки обусловили необходимость применения стохастического моделирования в экономическом анализе, называемого иначе математико-статистическими методами изучения связей, которые являются в определенной степени дополнением и углублением ДФА.
Таким образом, в экономическом анализе стохастические модели используются в тех случаях, когда необходимо:
– оценить влияние факторов, по которым нельзя построить жестко детерминированную модель;
– изучить и сравнить влияние факторов, которые нельзя включить в одну и ту же детерминированную модель;
– выделить и оценить влияние сложных факторов, которые не могут быть выражены одним определенным количественным показателем.
В отличие от детерминированного, стохастический подход для своей реализации требует выполнения ряда предпосылок:
1. Качественная однородность совокупности, т. е. в пределах варьирования значений факторов не должно происходить качественного скачка в характере отражаемого явления.
2. Достаточная численность совокупности наблюдения, позволяющая с точностью и надежностью выявить имеющиеся закономерности (в теории статистики считается, что количество наблюдений должно в 6-8 раз превышать количество факторов).
3. Наличие методов, т. е. специального математического аппарата, позволяющего выявить тесноту связи между изучаемыми показателями и оценить величину влияния факторов на изменение результативного показателя.
В целом стохастическое моделирование предназначено для решения трех задач:
1) установление факта наличия или отсутствия связи между изучаемыми признаками;
2) выявление причинных связей между изучаемыми показателями и количественное измерение действия факторов на результативный показатель;
3) прогнозирование неизвестных значений результативных показателей.
Проведение стохастического моделирования осуществляется согласно следующим этапам:
1) качественный анализ, подразумевающий постановку цели анализа, определение результативных и факторных признаков, отбор и отсев факторов;
2) количественный анализ, т. е. построение регрессионной модели (уравнения регрессии) и расчет параметров уравнений регрессии;
3) проверка адекватности модели, т. е. оценка точности (надежности) уравнения связи и правомерности его использования для практической цели.
Практическая реализация указанных этапов основывается на применении корреляционного и регрессионного методов анализа, рассмотренных ниже.
7.2 Методы стохастического моделирования
Методы стохастического моделирования включают в себя корреляционно-регрессионный анализ, в результате которого будут рассчитаны коэффициенты ее тесноты и значимости (т. е. проведен корреляционный анализ); будет построена регрессионная зависимость (т.е. проведен регрессионный анализ), позволяющая количественно измерить действия факторов на результативный показатель.
1. Корреляционный метод позволяет количественно выразить взаимосвязь между показателями. При этом если показатель зависит от одного фактора, то речь идет о парной корреляции, если он зависит от множества факторов, то о множественной корреляции. Основная особенность корреляционного анализа в том, что он устанавливает лишь факт наличия связи и степень ее тесноты, не вскрывая причины.
Задача корреляционного анализа – выявить тесноту связи изучаемых признаков, что осуществляется либо с помощью коэффициента корреляции (при прямолинейной зависимости), либо с помощью корреляционного отношения (при линейной и нелинейной зависимости).
Коэффициент корреляции (парный коэффициент корреляции, линейный коэффициент корреляции) между фактором х и результативным показателем Y определяется следующим образом:
где y – абсолютное значение результативного показателя; x – абсолютное значение фактора; n – количество наблюдений.
Коэффициент корреляции может принимать значения от –1 до +1. При этом если:
r = -1, то это означает наличие функциональной связи обратно-пропорционального характера;
r = +1, то это означает наличие функциональной связи прямо-пропорционального характера (и в этом и в другом случае переходят к детерминированному факторному анализу);
r = 0, то это означает отсутствие связи между фактором и изучаемым результативным показателем (фактор исключается из факторной системы);
Другие значения r свидетельствуют о наличии стохастической зависимости, причем чем больше /r/ стремится к 1, тем связь теснее. В частности:
/r/ < 0,3 означает слабую связь;
0,3 < /r/ < 0,7 – связь средней тесноты;
/r/ > 0,7 – связь тесная, т. е. имеется объективная возможность перейти к стохастическому факторному анализу.
При парной корреляции теснота связи изучается между результативным признаком и фактором.
В случае множественной корреляции тесноту связи между результативным показателем и набором факторов изучают на основе коэффициента множественной корреляции (R):
 ,
,
где – среднее значение результативного показателя, вычисленное по уравнению регрессии; – среднее значение результативного показателя, вычисленное по исходным данным.
Коэффициент множественной корреляции принимает только положительные значения в пределах от 0 до 1. При значении R≤0,3 говорят о малой зависимости между величинами, при значении 0,3 < R< 0,6 – о средней тесноте связи, при R>0,6 – о наличии существенной связи.
При множественной корреляции теснота связи изучается:
– между результативным признаком (функцией) и каждой переменной (аргументом);
– между переменными попарно.
Альтернативным показателем степени зависимости между двумя переменными является коэффициент детерминации, представляющий собой возведение в квадрат коэффициента корреляции (r 2 или R 2 – величина достоверности аппроксимации). Коэффициент детерминации, значение которого должно стремиться к 1, показывает, чему равна доля влияния изучаемого (изучаемых) фактора (факторов) на результативный показатель. При этом следует помнить, что при условии, если r 2 (или R 2)<0,5, синтезированные математические модели связи практического значения не имеют.
Практическая реализация корреляционного анализа включает следующие последовательные этапы:
1) постановка задач и выбор признаков;
2) формирование массива исходной статистической информации, определение степени ее однородности (на основе коэффициента вариации);
3) предварительная характеристика взаимосвязи (аналитические группировки, графики);
4) устранение мультиколлинеарности (взаимозависимости факторов), уточнение набора факторов (отбор наиболее существенных) на основе коэффициента корреляции, индекса детерминации или критерия Стьюдента (подробно см. п. 7.3). При этом в ходе отбора факторов следует придерживаться следующих правил:
– учитывать причинно-следственные связи между показателями (не рекомендуется включать в модель взаимосвязанные факторы: если парный коэффициент корреляции между двумя факторами больше 0,85, то один из них необходимо исключить).
– отбирать самые значимые факторы;
– рассматривать только те факторы, которые должны быть количественно измеримы, т. е. иметь единицу измерения и находить отражение в учете и отчетности;
– учитывать только однонаправленные факторы (т. е. при линейном характере зависимости нельзя включать в модель факторы, связь которых с результативным показателем имеет криволинейный характер);
После осуществления всех вышеуказанных процедур в случае установления факта высокой тесноты связи (> 0,7) приступают к решению второй задачи – регрессионному анализу, который позволяет выявить конкретные величины влияния факторов на изменение результативного показателя.
2. Регрессионный анализ – это метод установления аналитического выражения (т.е. уравнения регрессии) стохастической зависимости между исследуемыми признаками.
Уравнение регрессии показывает, как в среднем изменяется результативный признак (Y) при изменении любой из переменных (Х i) и имеет вид: Y = f (x 1 ,x 2,… x n),
где Y – зависимая переменная, т.е. результативный показатель; x i – независимые переменные (факторы).
В ходе регрессионного анализа решаются две главные задачи:
– построение уравнения регрессии, т. е. нахождение вида зависимости между результативным показателем и независимыми факторами;
– оценка значимости полученного уравнения (на основе коэффициента детерминации, критерия Фишера и критерия Стьюдента).
Вид уравнения регрессии определяется по графику, изображающему связь между факторами и результативным показателем, который строится на основе однородной совокупности статистических данных и служит обоснованием уравнения связи.
Если зависимость линейная (на графике изображена в виде прямой восходящей или снисходящей линии), то при:
а) однофакторном анализе уравнение будет иметь вид: Y(х) = а +b·x,
где Y – результативный показатель; b – коэффициент регрессии, который показывает, насколько изменится результативный показатель при изменении фактора на 1 ед.; а – свободный член, который показывает величину влияния неучтенных факторов; х – фактор;
б) многофакторном анализе уравнение будет иметь вид:
Y(х) = а +b 1 x 1 + b 2 x 2 +…+ b n x n.
Если зависимость нелинейная (на графике изображена в виде параболы или гиперболы), то уравнение регрессии принимает следующий вид:
Y(х) = а +b·x + с·x 2 – при графике в виде параболы;
Y(х) = а +b:x 2 – при графике в виде гиперболы.
При сложном характере зависимости между изучаемыми явлениями используются более сложные параболы (третьего, четвертого порядка (полинома) и т. д.), а также квадратическое, степенные, показательные и другие функции.
Выбор конкретного уравнения регрессии и его решение осуществляется в рамках табличного процессора MS Excel или статистического программного пакета STADIA.
Сущность решения уравнений регрессии заключается в нахождении параметров регрессии (а и b). Это осуществляется по способу наименьших квадратов с использованием системы нормальных уравнений, суть которого заключается в минимизации суммы квадратов отклонений фактических значений результативного показателя от его расчетных значений.
При прямолинейной зависимости система нормальных уравнений имеет вид:
∑y = na +b∑x
∑xy = a∑x +b∑x 2 .
При криволинейной зависимости:
∑y(1/x)= a∑1/x +b∑(1/x) 2 .
Для оценки адекватности модели используют такие критерии, как ошибка аппроксимации, F-отношения, коэффициента детерминации, подробно рассмотренные в п. 7.3.
В необходимых случаях построение уравнения регрессии может быть использовано для прогнозирования результативного признака.
Апробируем методику корреляционно-регрессионного анализа на конкретном примере.
Пример 7.1 На основании данных табл. А необходимо проанализировать зависимость между расходами на оплату труда (Y) и выручкой от продажи товаров (х).
Таблица А – Данные о выручке от продажи товаров и сумме расходов на оплату труда в разрезе торговых организаций тыс. руб.
| № мага-зинов | Выручка от продажи товаров | № магазинов | Выручка от продажи товаров | Сумма расходов на оплату труда | |
| А | 1 | 2 | Б | 3 | 4 |
| 1. | 3 200 | 190 | 15. | 1 690 | 177 |
| 2. | 500 | 45 | 16. | 7 450 | 230 |
| 3. | 12 000 | 670 | 17. | 12 900 | 587 |
| 4. | 8 560 | 345 | 18. | 2 010 | 166 |
| 5. | 14 100 | 713 | 19. | 1 650 | 105 |
| 6. | 11 300 | 470 | 20. | 5 115 | 241 |
| 7. | 4 300 | 194 | 21. | 8 945 | 400 |
| 8. | 1 010 | 98 | 22. | 11 900 | 523 |
| 9. | 8 230 | 244 | 23. | 14 200 | 780 |
| 10. | 12 560 | 510 | 24. | 10 300 | 576 |
| 11. | 6 201 | 215 | 25. | 11 450 | 425 |
| 12. | 11 500 | 603 | 26. | 13 000 | 606 |
| 13. | 13 300 | 575 | 27. | 6 100 | 210 |
| 14. | 1 000 | 95 | 28. | 7 500 | 249 |
На основании данных табл. А построим график зависимости изменения расходов на оплату труда от изменения товарооборота (см. рисунок).

Зависимость динамики расходов на оплату труда от выручки от продажи товаров
Данные графика свидетельствуют о том, что между расходами на оплату труда и выручкой от продажи товаров существует прямолинейная зависимость. Далее измерим тесноту связи между изучаемыми показателями на основе коэффициента корреляции, для чего сгруппируем магазины по сумме выручки от продажи товаров (см. тему 3) и составим следующую разработочную таблицу (табл. Б).
Таблица Б – Разработочная таблица для определения показателей, используемых при расчете коэффициента корреляции
| Группы магазинов по сумме выручки от продажи товаров | Количество магазинов | Выручка от продажи товаров (x i), млн руб. | Сумма расходов на оплату труда (y i), млн руб. | |||
| От 500 до 3 220 включ. | 7,000 | 11,060 | 0,876 | 9,689 | 122,324 | 0,768 |
| От 3 221 до 5 440 включ. | 2,000 | 9,415 | 0,435 | 4,096 | 88,642 | 0,190 |
| От 5 441 до 8 160 включ. | 4,000 | 27,251 | 0,904 | 24,635 | 742,617 | 0,818 |
| От 8 161 до 10 880 включ. | 4,000 | 36,035 | 1,565 | 56,394 | 1298,521 | 2,450 |
| Св. 10 881 | 11,000 | 138,210 | 5,859 | 809,772 | 19102,004 | 34,328 |
| Итого | 28,000 | 221,971 | 9,639 | 904,586 | 21354,107 | 38,550 |
Примечание. Согласно данным таблицы, элементы расчета коэффициента корреляции имеют следующие значения:
Σx i = 221,971;
Σy i = 9,639; Σy i x i =904,586; Σx 2 i = 21 354,107; Σy 2 = 38,550.
Рассчитанные данные подставляются в формулу коэффициента корреляции:
r = 
Коэффициент детерминации: r 2 =0,8 2 =0,64.
Коэффициент корреляции, равный 0,8 ед., означает наличие высокой стохастической зависимости между суммой расходов на оплату труда и выручкой от реализации. Образование данной стохастической зависимости объясняется наличием (и доминированием в данном случае) постоянной части расходов по заработной плате, начисление которой не увязано с динамикой результата хозяйственной деятельности организации, т. е. выручки от продажи, а значение коэффициента детерминации, составляющее 0,64 ед. означает, что изменение расходов на оплату труда на 64 % объясняется изменением выручки от продажи, что дает основание для проведения регрессионного анализа.
Согласно виду графика, представленного на рисунке, между изучаемыми показателями существует прямолинейная корреляционная зависимость, в связи с чем уравнение регрессии будет иметь вид: Y(х) = а +b·x,
где Y – расходы на оплату труда; х – выручка от продажи товаров.
Для определения параметров а и в следует решить систему нормальных уравнений методом наименьших квадратов:
∑y = na +b∑x
∑xy = a∑x +b∑x 2 .
Отсюда значения коэффициента в определяется по формуле
Рассчитанное значение параметра в говорит о том, что при увеличении выручки от продажи товаров на 1 млн руб. расходы на оплату труда возрастут на 42,3 тыс. руб. При этом подставив значение данного параметра в первое уравнение системы, определим значение параметра а:
∑y = na +b∑x
9,639=а·28+0,0423·221,971
28а=0,0423·221,971-9,639
Значение параметра а показывает, что коэффициент регрессии может быть применим для торговых организаций с размером выручки от продажи за год свыше 9 млн. руб.
В целом уравнение регрессии имеет вид: y = 0,009+0,0423·х.
Полученное уравнение связи можно использовать для прогнозирования суммы расходов на оплату труда, если выручка от продажи возрастет и составит, например, 15 млн руб.:
y = 0,009+0,0423·х=0,009+0,0423·15=0,644 млн. руб.
7.3 Критерии оценки адекватности результатов стохастического анализа
При выполнении регрессионного анализа необходимо получить оценки, позволяющие оценить точность модели, вероятность ее существования и обоснованность применения в аналитических целях. Таким образом, качество корреляционно-регрессионного анализа обеспечивается выполнением ряда следующих условий:
1. Однородность исходной информации, которая оценивается в зависимости от относительного ее распределения около среднего значения. Критериями здесь служат (подробно см. тему 3):
– среднеквадратическое отклонение;
– коэффициент вариации;
– коэффициент равномерности;
– закон нормального распределения.
2. Значимость коэффициентов корреляции может быть оценена (наряду с уже указанным выше коэффициентом детерминации) с помощью t-критерия Стьюдента, алгоритм расчета которого при линейной однофакторной связи имеет вид:
 .
.
Если полученное эмпирическое (расчетное) значение критерия (t э) будет больше критического табличного значения (t т), то коэффициент корреляции можно признать значимым.
3. Адекватность (надежность) уравнения регрессии оценивается с помощью F-критерия Фишера, алгоритм расчета которого выглядит следующим образом:
 ,
,
где m – число параметров уравнения регрессии; σ 2 y – дисперсия по линии регрессии; σ 2 ост – остаточная дисперсия.
Если эмпирическое значение F-критерия (F э) окажется выше табличного (F т), то уравнение регрессии следует признать адекватным, т. е. правомерным для использования. При этом чем выше величина критерия Фишера, тем точнее в уравнении связи представлена зависимость, сложившаяся между факторными и результативными показателями.
4. Сравнительная сила влияния факторов, оценка которой необходима с целью определения проблемной и наиболее эффективной в перспективе зоны для направления усилий в конкретную область бизнеса. Решение этой задачи может быть осуществимо посредством использования:
а) частных коэффициентов эластичности (Э i), показывающих ожидаемый рост результативного показателя (в %) с возрастанием факторного на 1 %:

б) стандартизированных бета-коэффициентов (β i):

Чем выше бета-коэффициент, тем сильнее воздействие анализируемого фактора на результативный признак.
Тесты для самоконтроля знаний по теме 7
1. Коэффициент корреляции, равный 0, означает:
б) наличие функциональной связи прямо-пропорционального характера;
2. Коэффициент корреляции, равный (-1), означает:
а) наличие функциональной связи обратно пропорционального характера;
б) наличие функциональной связи прямо пропорционального характера;
в) отсутствие связи между фактором и изучаемым результативным показателем.
3. О наличии стохастической зависимости свидетельствует значение коэффициента корреляции, равное:
г) другие значения.
4. Аналитическая задача, которую позволяют решить методы стохастического моделирования:
а) установление факта наличия или отсутствия связи между изучаемыми признаками;
б) выявление общей тенденции изменения изучаемого показателя;
в) выбор оптимального варианта решения проблемы;
г) количественно оценка влияния факторов, находящихся с результативным показателем в функциональной зависимости.
5. Выявить тесноту связи факторных показателей и результативного позволяет:
а) корреляционный анализ;
б) регрессионный анализ;
в) детерминированный анализ.
6. Метод установления аналитического выражения (уравнения) стохастической зависимости между исследуемыми признаками – это … анализ.
7. В ходе регрессионного анализа решается следующая аналитическая задача:
а) нахождение вида зависимости между результативным показателем и независимыми факторами;
б) выявление тесноты связи факторных показателей и результативного;
в) количественная оценка влияния факторов, находящихся с результативным показателем в функциональной зависимости.
8. Для оценки достоверности полученного уравнения регрессии используют:
а) коэффициент детерминации;
б) критерий Фишера;
в) критерий Стьюдента;
г) коэффициент Кенделя;
д) коэффициент долевого участия интенсивных факторов;
е) коэффициент ритмичности;
ж) коэффициент экстенсивности.
9. При линейной однофакторной зависимости уравнение регрессии будет иметь вид:
а) y (х) = а +b·x;
б) y (х) = а +b 1 ·x 1 + b 2* x 2 +…+ b n ·x n ;
в) y (x) = a+в:х.
10. При линейной многофакторной зависимости уравнение регрессии будет иметь вид:
а) y(х) = а +b·x;
б) y (х) = а +b 1 ·x 1 + b 2 ·x 2 +…+ b n ·x n ;
в) y (x) = a+в:х.
11. В уравнении регрессии вида y(х) = а +b·x y – это:
а) результативный показатель;
б) коэффициент регрессии;
в) свободный член.
12. В уравнении регрессии вида y(х) = а +b·x а – это:
а) результативный показатель
б) коэффициент регрессии;
в) свободный член.
13. Коэффициент регрессии (b) в уравнении регрессии вида y(х) = а +b·x показывает:
а) на сколько изменится значение результативного показателя при изменении фактора на единицу;
б) величину влияния неучтенных факторов.
14. Если полученное эмпирическое (расчетное) значение критерия Стьюдента (t э) будет больше критического табличного значения (t т), то коэффициент корреляции … признать значимым.

Международной политике и законодательству. 10. Анализ должен быть эффективным, т.е. затраты на его проведение должны давать многократный эффект. 4. ЭКОНОМИЧЕСКИЙ АНАЛИЗ В ДЕЯТЕЛЬНОСТИ ОВД Содержание, цели и задачи экономико-финансового анализа, проводимого органами внутренних дел В рыночных условиях проведения социально-экономических реформ в деятельности органов внутренних дел по...
Моделирование – построение моделей для исследования и изучения объектов, процессов, явлений.
стохастическое моделирование отображает вероятностные процессы и события. В этом случае анализируется ряд реализаций случайного процесса, и оцениваются средние характеристики.
один подход к классификации математических моделей подразделяет их на детерминированные истохастические (вероятностные). В детерминированных моделях входные параметры поддаются измерению однозначно и с любой степенью точности, т.е. являются детерминированными величинами. Соответственно, процесс эволюции такой системы детерминирован. В стохастических моделях значения входных параметров известны лишь с определенной степенью вероятности, т.е. эти параметры являются стохастическими; соответственно, случайным будет и процесс эволюции системы. При этом, выходные параметры стохастической модели могут быть как величинами вероятностными, так и однозначно определяемыми.
В зависимости от характера исследуемых реальных процессов и систем математические модели могут быть:
детерминированные,
стохастические.
В детерминированных моделях предполагается отсутствие всяких случайных воздействий, элементы модели (переменные, математические связи) достаточно точно установленные, поведение системы можно точно определить. При построении детерминированных моделей чаще всего используются алгебраические уравнения, интегральные уравнения, матричная алгебра.
Стохастическая модель учитывает случайный характер процессов в исследуемых объектах и системах, который описывается методами теории вероятности и математической статистики.
Типовые схемы. Приведенные математические соотношения представляют собой математические схемы общего вида и позволяют описать широкий класс систем. Однако в практике моделирования объектов в области системотехники и системного анализа на первоначальных этапах исследования системы рациональнее использовать типовые математические схемы.
В качестве детерминированных моделей, когда при исследовании случайные факторы не учитываются, для представления систем, функционирующих в непрерывном времени, используются дифференциальные, интегральные, интегродифференциальные и другие уравнения, а для представления систем, функционирующих в дискретном времени, конечные автоматы и конечно-разностные схемы.
В качестве стохастических моделей (при учете случайных факторов) для представления систем с дискретным временем используются вероятностные автоматы, а для представления системы с непрерывным временем – системы массового обслуживания и т. д.
Перечисленные типовые математические схемы, естественно, не могут претендовать на возможность описания на их базе всех процессов, происходящих в больших системах. Для таких систем в ряде случаев более перспективным является применение агрегативных моделей. Агрегативные модели (системы) позволяют описать широкий круг объектов исследования с отображением системного характера этих объектов. Именно при агрегативном описании сложный объект (система) расчленяется на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие взаимодействие частей.
Таким образом, при построении математических моделей процессов функционирования систем можно выделить следующие основные подходы:
непрерывно-детерминированный (например, дифференциальные уравнения);
дискретно-детерминированный (конечные автоматы);
дискретно-стохастический (вероятностные автоматы);
непрерывно-стохастический (системы массового обслуживания);
обобщенный, или универсальный (агрегативные системы).
20. Модель популяции .
Модель – это мысленно представляемая или материально реализованная система, которая, отображая или воспроизводя объект исследования, способна замещать его так, что ее изучение дает новую информацию о нем. Рассмотрим примеры динамических систем - модели популяций. Популяция (от лат.populatio- население) - термин, используемый в различных разделах биологии, а также в генетике, демографии и медицине.
Популяция - это человеческое, животное или растительное население некоторой местности, способной к более-менее устойчивому самовоспроизводству, относительно обособленное (обычно географически) от других групп.
Описание популяций, а также происходящих в них и с ними процессов, возможно путем создания и исследования динамических моделей.
Пример 1. Модель Мальтуса.
Скорость роста пропорциональна текущему размеру популяции. Она описывается дифференциальным уравнением х = ах , где α - некоторый параметр, определяемый разностью между рождаемостью и смертностью. Решением этого уравнения является экспоненциальная функцияx(t) = х 0 е*.
Если рождаемость превосходит смертность (α > 0), размер популяция неограниченно и очень быстро возрастает. Понятно, что в действительности этого не может происходить из-за ограниченности ресурсов. При достижении некоторого критического объема популяции модель перестает быть адекватной, поскольку не учитывает ограниченность ресурсов. Уточнением модели Мальтуса может служить логистическая модель, которая описывается дифференциальным уравнением Ферхюльста:
где x s - «равновесный» размер популяции, при котором рождаемость в точности компенсируется смертностью. Размер популяции в такой модели стремится к равновесному значению
Пример 2. Модель «хищник - жертва».
Модель взаимодействия «хищник - жертва» независимо предложили в 1925 - 1927 гг. Лотка и Вольтерра. Два дифференциальных уравнения моделируют временную динамику численности двух биологических популяций жертвы и хищника. Предполагается, что жертвы размножаются с постоянной скоростью а их численность убывает вследствие поедания хищниками. Хищники же размножаются со скоростью, пропорциональной количеству пищи и умирают естественным образом.
Допустим, что на некоторой территории обитают два вида животных: кролики (питающиеся растениями) и лисы (питающиеся кроликами). Пусть число кроликов -х, число лис -у. Используя модель Мальтуса с необходимыми поправками, учитывающими поедание кроликов лисами, приходим к следующей системе, носящей имя модели Вольтерра - Лотки:
х =(α -су)х;
Эта система имеет равновесное состояние, когда число кроликов и лис постоянно. Отклонение от этого состояния приводит к колебаниям численности кроликов и лис, аналогичным колебаниям гармонического осциллятора. Как и в случае гармонического осциллятора, это поведение не является структурно устойчивым: малое изменение модели (например, учитывающее ограниченность ресурсов, необходимых кроликам) может привести к качественному изменению поведения. Например, равновесное состояние может стать устойчивым, и колебания численности будут затухать. Возможна и противоположная ситуация, когда любое малое отклонение от положения равновесия приведет к катастрофическим последствиям, вплоть до полного вымирания одного из видов.
МАТЕМАТИЧЕСКИЕ МОДЕЛИ
2.1. Постановка задачи
Детерминированные модели описывают процессы в детерминированных системах.
Детерминированные системы характеризуются однозначным соответствием (соотношением) между входными и выходными сигналами (процессами).
Если задан входной сигнал такой системы, известны ее характеристика y = F(x), а также ее состояние в начальный момент времени, то значение сигнала на выходе системы в любой момент времени определяется однозначно (рис. 2.1).
Существует два подхода к исследованию физических систем: детерминированный и стохастический.
Детерминированный подход основан на применении детерминированной математической модели физической системы.
Стохастический подход подразумевает использование стохастической математической модели физической системы.
Стохастическая математическая модель наиболее адекватно (достоверно) отображает физические процессы в реальной системе, функцио-нирующей в условиях влияния внешних и внутренних случайных факторов (шумов).
2.2. Случайные факторы (шумы)
Внутренние факторы −
1) температурная и временная нестабильность электронныхкомпонентов;
2) нестабильность питающего напряжения;
3) шум квантования в цифровых системах;
4) шумы в полупроводниковых приборах в результате неравномерности процессов генерации и рекомбинации основных носителей заряда;
5) тепловой шум в проводниках за счет теплового хаотического движения носителей заряда;
6) дробовой шум в полупроводниках, обусловленный случайным характером процесса преодоления носителями потенциального барьера;
7) фликкер – шум, обусловленный медленными случайными флуктуациями физико-химического состояния отдельных областей материалов электронных устройств и т. д.
Внешние факторы –
1) внешние электрические и магнитные поля;
2) электромагнитные бури;
3) помехи, связанные с работой промышленности и транспорта;
4) вибрации;
5) влияние космических лучей, тепловое излучение окружающих объектов;
6) колебания температуры, давления, влажности воздуха;
7) запыленность воздуха и т. д.
Влияние (наличие) случайных факторов приводит к одной из ситуаций, приведенных на рис. 2.2:
С ледовательно,
предположение о детерминированном
характере физической системы и описание
ее детерминированной математической
моделью является идеализацией
реальной системы.
Фактически
имеем ситуацию, изображенную на рис.
2.3.
ледовательно,
предположение о детерминированном
характере физической системы и описание
ее детерминированной математической
моделью является идеализацией
реальной системы.
Фактически
имеем ситуацию, изображенную на рис.
2.3.
Детерминированная модель допустима в следующих случаях:
1) влияние случайных факторов столь незначительно, что пренебрежение ими не приведет к ощутимому искажению результатов моделирования.
2 )
детерминированная
математическая модель отображает
реальные физические процессы в
усредненном смысле.
)
детерминированная
математическая модель отображает
реальные физические процессы в
усредненном смысле.
В тех задачах, где не требуется высокой точности результатов моделирования, предпочтение отдается детерминированной модели. Это объясняется тем, что реализация и анализ детерминированной математической модели много проще, чем стохастической.
Детерминированная модель недопустима в следующих ситуациях: случайные процессы ω(t) соизмеримы с детерминированными x(t). Результаты, полученные с помощью детерминированной математической модели, будут неадекватными реальным процессам. Это относится к системам радиолокации, к системам наведения и управления летательными аппаратами, к системам связи, телевидению, к системам навигации, к любым системам, работающим со слабыми сигналами, в электронных устройствах контроля, в прецизионных измерительных устройствах и т. д.
В математическом моделировании случайный процесс часто рассматривают как случайную функцию времени, мгновенные значения которой являются случайными величинами.
2.3. Суть стохастической модели
Стохастическая математическая модель устанавливает вероятностные соотношения между входом и выходом системы . Такая модель позволяет сделать статистические выводы о некоторых вероятностных характеристиках исследуемого процесса y(t):
1) математическое ожидание (среднее значение):
2) дисперсия (мера рассеивания значений случайного процесса y(t) относительно его среднего значения):
3) среднее квадратичное отклонение:
 (2.3)
(2.3)
4) корреляционная функция (характеризует степень зависимости – корреляции – между значениями процесса y(t), отстоящими друг от друга на время τ):
5) спектральная плотность случайного процесса y(t) описывает его частотные свойства:
 (2.5)
(2.5)
преобразование Фурье.
Стохастическаямодель формируется на основе стохастического дифференциального либо стохастического разностного уравнения.
Различают три типа стохастических дифференциальных уравнений: со случайными параметрами, со случайными начальными условиями, со случайным входным процессом (случайной правой частью). Приведем пример стохастического дифференциального уравнения третьего типа:
 ,
(2.6)
,
(2.6)
где
 – аддитивный
случайный процесс – входной шум.
– аддитивный
случайный процесс – входной шум.
В нелинейных системах присутствуют мультипликативные шумы .
Анализ стохастических моделей требует использования довольно сложного математического аппарата, особенно для нелинейных систем.
2.4. Понятие типовой модели случайного процесса. Нормальный (гауссовский) случайный процесс
При разработке
стохастической модели важное значение
имеет определение характера случайного
процесса
 .
Случайный процесс может быть описан
набором (последовательностью) функций
распределения – одномерной, двумерной,
… , n-мерной
или соответствующими плотностями
распределения вероятности. В большинстве
практических задач ограничиваются
определением одномерного и двумерного
законов распределения.
.
Случайный процесс может быть описан
набором (последовательностью) функций
распределения – одномерной, двумерной,
… , n-мерной
или соответствующими плотностями
распределения вероятности. В большинстве
практических задач ограничиваются
определением одномерного и двумерного
законов распределения.
В некоторых
задачах характер распределения
 априорно известен.
априорно известен.
В
большинстве случаев, когда случайный
процесс
 представляет собой результат воздействия
на физическую систему совокупности
значительного числа независимых
случайных факторов, полагают, что
представляет собой результат воздействия
на физическую систему совокупности
значительного числа независимых
случайных факторов, полагают, что
 обладает свойствами нормального
(гауссовского) закона распределения
.
В
этом случае говорят, что случайный
процесс
обладает свойствами нормального
(гауссовского) закона распределения
.
В
этом случае говорят, что случайный
процесс
 заменяется его
типовой
моделью
–
гауссовским случайным процессом.
Одномерная
плотность
распределения
вероятности
нормального
(гауссовского)случайного
процесса приведена на рис. 2.4.
заменяется его
типовой
моделью
–
гауссовским случайным процессом.
Одномерная
плотность
распределения
вероятности
нормального
(гауссовского)случайного
процесса приведена на рис. 2.4.
Нормальное (гауссовское) распределение случайного процесса обладает следующими свойствами .
1. Значительное количество случайных процессов в природе подчиняются нормальному (гауссовскому) закону распределения.
2. Возможность достаточно строго определить (доказать) нормальный характер случайного процесса.
3. При воздействии на физическую систему совокупности случайных факторов с различными законами распределения их суммарный эффект подчиняется нормальному закону распределения (центральная предельная теорема ).
4. При прохождении через линейную систему нормальный процесс сохраняет свои свойства в отличие от других случайных процессов.
5. Гауссовский случайный процесс может быть полностью описан с помощью двух характеристик – математического ожидания и дисперсии.
В процессе моделирования часто возникает
задача – определить
характер распределения
некоторой случайной величины x по
результатам её многократных измерений
(наблюдений)
процессе моделирования часто возникает
задача – определить
характер распределения
некоторой случайной величины x по
результатам её многократных измерений
(наблюдений)
 .
Для
этого составляют гистограмму
– ступенчатый график, позволяющий по
результатам измерения случайной величины
оценить её плотность распределения
вероятности.
.
Для
этого составляют гистограмму
– ступенчатый график, позволяющий по
результатам измерения случайной величины
оценить её плотность распределения
вероятности.
При построении
гистограммы диапазон значений случайной
величины
 разбивают на некоторое количество
интервалов, а затем подсчитывают частоту
(процент) попадания данных в каждый
интервал. Таким образом, гистограмма
отображает частоту попадания значений
случайной величины в каждый из интервалов.
Если аппроксимировать построенную
гистограмму непрерывной аналитической
функцией, то эта функция может
рассматриваться как статистическая
оценка неизвестной теоретической
плотности распределения вероятности.
разбивают на некоторое количество
интервалов, а затем подсчитывают частоту
(процент) попадания данных в каждый
интервал. Таким образом, гистограмма
отображает частоту попадания значений
случайной величины в каждый из интервалов.
Если аппроксимировать построенную
гистограмму непрерывной аналитической
функцией, то эта функция может
рассматриваться как статистическая
оценка неизвестной теоретической
плотности распределения вероятности.
При формировании непрерывных стохастических моделей используется понятие «случайный процесс». Разработчики разностных стохастических моделей оперируют понятием «случайная последовательность».
Особую роль в теории стохастического моделирования играют марковские случайные последовательности. Для них справедливо следующее соотношение для условной плотности вероятности:
Из
него следует, что вероятностный закон,
описывающий поведение процесса в момент
времени
 ,
зависит только от предыдущего состояния
процесса в момент времени
,
зависит только от предыдущего состояния
процесса в момент времени
 и абсолютно не зависит от его поведения
в прошлом (т. е. в моменты времени
и абсолютно не зависит от его поведения
в прошлом (т. е. в моменты времени
 ).
).
Перечисленные выше внутренние и внешние случайные факторы (шумы) представляют собой случайные процессы различных классов. Другими примерами случайных процессов являются турбулентные течения жидкостей и газов, изменение нагрузки энергосистемы, питающей большое количество потребителей, распространение радиоволн при наличии случайных замираний радиосигналов, изменение координат частицы в броуновском движении, процессы отказов аппаратуры, поступления заявок на обслуживание, распределение числа частиц в малом объеме коллоидного раствора, задающее воздействие в радиолокационных следящих системах, процесс термоэлектронной эмиссии с поверхности металла и т. д.