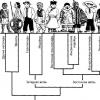
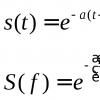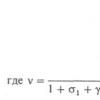Анализ поведения системы при помощи показателей ляпунова. Что такое показатели ляпунова. Численное определение показателей Ляпунова
Одной из важнейших количественных характеристик хаотических процессов является характеристический показатель Ляпунова (λ ). Как уже говорилось, в пределах аттрактора небольшие изменения начальных условий могут приводить к сильным изменениям в эволюции системы. Характеристический показатель Ляпунова может являться мерой того, насколько сильны могут быть эти изменения. Чем чувствительнее система к начальным условиям, тем он больше. Поскольку в n -мерном фазовом пространстве есть n независимых направлений, то систему характеризуют n характеристических показателей Ляпунова. Вычисляется обычно наибольший из них. Существует алгоритм вычисления этой величины, не требующий восстановления аттрактора, что значительно ускоряет вычисления . Используется метод задержек. Реконструируемая траектория X может быть выражена как матрица, где каждому ряду соответствует фазово-пространственный вектор:
X= [X 1 X 2 … X M ] T ,
где X i – состояние системы в момент времени i . Для N временных выборок {x 1 , x 2 , …, x N }, каждому X i соответствует
X i = [x i x i+J … x i+(m-1)J ],
где J – задержка реконструкции, m – размерность вложения. Таким образом, X – это матрица M × m , а константы m , M и N связаны следующим соотношением
M=N – (m – 1 )J.
Размерность вложения обычно оценивается в соответствии с теоремой Такенса m >2 n , хотя этот алгоритм работает и при значениях m ниже критерия Такенса.
После реконструкции динамики системы находим ближайшего «соседа» для каждой точки траектории. Ближайшего «соседа» X j ’ определяем как точку, которая минимизирует расстояние до особой точки касания X j :
d j (0)=min ||X j -X j ’ ||,
где d j (0) – расстояние от j -й точки до ее ближайшего «соседа», а || || – означает евклидову норму. Сделано следующее допущение: ближайшие «соседи» имеют временной интервал больший, чем средний период временного ряда Т ср. :
|j - j ’ |>Т ср
Это позволяет предположить, что каждая пара соседей является начальными условиями для разных траекторий. Наибольший характеристический показатель Ляпунова оценивается как среднее значение временного интервала между ближайшими «соседями».
Характеристический показатель Ляпунова может быть как положительным, так и отрицательным. Все характеристические показатели Ляпунова детерминированного процесса отрицательны или равны нулю; у хаотических процессов хотя бы один (старший) положителен.
Результаты расчетов набора характеристических показателей Ляпунова показаны на рисунке 3.73.
Рисунок 3.73. Набор характеристических показателей Ляпунова, i – номер показателя. Применены следующие условные обозначения:

На рис. 3.73 показаны рассчитанные значения характеристических показателей Ляпунова для участков нативных сигналов ЭЭГ. Следует оговориться, что приведены три показателя, хотя расчет проводился для разного количества, в соответствии с определенной ранее внедренной размерностью методом ближайших «ложных соседей» (см. табл. 3.3). Диапазон значений i составил от 3 до 9, поэтому для единообразия представления оставлены три первых значения.
Диагностическое значение имеет только первый (старший, максимальный) показатель Ляпунова, и не столько его абсолютная величина, а знак – положительный или отрицательный.
В соответствии с условиями проведения измерений и для обеспечения повторяемости и статистической значимости результатов было сделано несколько выборок для каждого сигнала (по 20 выборок). Затем была выполнена статистическая обработка результатов по стандартным методиками обработки результатов измерений . Полученные результаты для старшего показателя сведены в таблицу 3.6.
Таблица 3.6
Максимальный характеристический показатель Ляпунова для исследуемых нативных ЭЭГ сигналов
|
Максимальный показатель Ляпунова, λ, с -1 | ||
|
Здоровые | ||
Основной вывод, который может быть сделан из данных исследований - так как первая экспонента характеристического показателя Ляпунова положительная, то в системе присутствует хаос.
Что касается абсолютных значений максимального характеристического показателя Ляпунова, то можно сказать, что он не показывает значительной вариабельности для набора исследуемых случаев. Для условно здоровых пациентов величина λ 1 немного выше, чем для пациентов с различными заболеваниями, в среднем на 0,1 с -1 . Это говорит о большей степени хаотичности сигнала для мозга в условно здоровом состоянии.
В случае игровой зависимости выявлена устойчивая тенденция к увеличению значения λ 1 , в то время как для здоровых пациентов абсолютное значение λ 1 было ниже на 0,3-0,5 с -1 . Это, скорее всего, связано с тем, что за каждое конкретное психическое заболевание отвечает конкретный участок мозга, ЭЭГ которого и необходимо тщательно исследовать. В данной работе, как было описано в разделе 3.1, применялись стандартные методики наложения электродов.
Опытным путем было обнаружено, что длинный – более 4 с – ЭЭГ сигнал проявляет в основном статистические свойства, обнаруживая удовлетворительную корреляцию (0,9 и выше). Хаотические свойства ЭЭГ сигналов удается обнаружить на выборках длительностью менее 1 с.
Исследования различных типов сигналов показали, что чем сложнее аттрактор системы, тем в более спокойном и здоровом состоянии находится мозг человека. При этом фрактальная размерность принимает значения в диапазоне 2-4, следовательно, по теореме Мане внедренная размерность сигнала составит целую часть D emb =, т.е. 5-9. Системы, описываемые такими сигналами, относят к сложным, высокоразмерным и их можно считать хаотическими.
Санкт-Петербургский государственный университет
Ключевые слова
комитеты искусственных нейронных сетей, локальные и глобальные показатели Ляпунова, реконструированные аттракторы, рекуррентное QR-разложение, временные ряды, аппроксимация динамической системы, Committees of artificial neural networks, local and global Lyapunov exponents, reconstructed attractors, recurrent QR-decomposition, time series, approximation of a dynamical system
Просмотр статьи
⛔️ (обновите страницу, если статья не отобразилась)Аннотация к статье
Предложен новый метод определения локальных и глобальных показателей Ляпунова по заданному временному ряду. Особенностью предложенного метода является использование комитета нейронных сетей для аппроксимации динамической системы, порождающей временной ряд. Аппроксимирующей моделью динамической системы служит обученная нейронная сеть. Комитеты сетей используются для повышения точности вычисления локальных и глобальных показателей Ляпунова. Показано, что на модельных временных рядах предложенный метод определяет все показатели Ляпунова динамической системы с хорошей точностью.
Текст научной статьи
Введение Показатели Ляпунова являются важной характеристикой динамических систем и описывают разбегание близлежащих траекторий динамической системы на аттракторе в фазовом пространстве или на реконструированном аттракторе. По известным показателям Ляпунова можно определить в каком режиме находится динамическая система: если старший показатель положителен, то данная динамическая система находится в хаотическом режиме. В настоящее время существует достаточно большое количество методов численных расчетов наибольших показателей Ляпунова для различных ситуаций . Однако в любом случае эти расчеты требуют наличия множества фазовых траекторий на аттракторе, которые в определенные моменты времени локализованы в достаточно малых фазовых объемах. Среди численных алгоритмов для расчета наибольший показатель Ляпунова непосредственно из временных рядов отметим, например, алгоритм Вольфа , алгоритм Сано и Савада и алгоритм Экмана . Следует, однако, заметить, что перечисленные алгоритмы и их модификации позволяют вычислить лишь старший показатель Ляпунова и, кроме того, вычисления по этим алгоритмам приводит, как правило, к неприемлемо большим погрешностям вычислений. Отметим также работы и , посвященные вычислению показателей Ляпунова или их аналогов с использованием нейросетевых технологий. Однако подход, использованный в настоящей работе, существенно отличается от методов работ и . Целью настоящей работы является разработка и тестирование на модельных временных рядах метода вычисления всех ляпуновских показателей по временному ряду с высокой точностью. Особенностью метода является использование комитета нейронных сетей для аппроксимации динамической системы, порождающей временной ряд. Как показано в настоящей работе, это позволяет преодолеть трудности численных алгоритмов, перечисленных выше. В начале настоящей работы приводятся определения локальных показателей Ляпунова (ЛПЛ) и глобальных показателей Ляпунова (ГПЛ). Затем рассматривается метод определения ГПЛ и ЛПЛ если известно отображение, задающее дискретную по времени динамическую систему. Далее рассматриваются способы обобщения данного метода на случай когда известен только временной ряд, порожденный дискретной динамической системой. После чего подробно описывается метод определения ЛПЛ по временному ряду с использованием нейронных сетей. В конце работы приведен обзор результатов применения предложенного метода к модельным временным рядам. Глобальные и локальные показатели Ляпунова Рассмотрим дискретную по времени динамическую систему, эволюция которой задается уравнением: Здесь - точки траектории динамической системы, - задает нумерацию точек траектории, - отображение задающее эволюцию траектории динамической системы. Рассмотрим как меняется малое возмущение траектории с течением времени. Пренебрегая старшими членами в ряде Тейлора для получим следующую оценку динамики возмущения: Здесь - матрица Якоби размера вычисленная в точке. Итеративно применяя последнюю формулу можно получить следующие соотношение: Здесь матрица описывает изменение во времени возмущения для шагов итераций. Если принадлежит аттрактору динамической системы, то при определенных условиях согласно при собственные числа матрицы не зависят от начальной точки и позволяют определить глобальные показатели Ляпунова следующим образом: Определение 1. Пусть - собственные числа матрицы при и для любой точки траектории, принадлежащей аттрактору динамической системы. Тогда - глобальные показатели Ляпунова (ГПЛ). При конечном собственные числа матрицы зависят от и. Можно ввести в рассмотрение локальные показатели Ляпунова: Определение 2. Пусть - собственные числа матрицы при конечном и для некоторой точки траектории. Тогда - локальные показатели Ляпунова (ЛПЛ) вычисленные за временных шагов для возмущения точки траектории. QR-алгоритм определения показателей Ляпунова Как было отмечено выше для определения локальных и глобальных показателей Ляпунова необходимо устойчиво вычислять собственные числа матрицы. Основная проблема связана с тем, что матрица плохо обусловлена при больших, и, как следствие, прямое вычисление матрицы, а затем и её собственных чисел, затруднительно. Однако можно учесть тот факт, что для определения показателей Ляпунова необходимы логарифмы собственных чисел. В работе предложен метод оценки логарифмов собственных чисел с помощью рекуррентного QR-разложения компонент матрицы. Первым шагом QR-алгоритма является выбор точки траектории и вычисление соответствующей ей матрицы Якоби. Далее производится QR-разложение на произведение двух матриц: , где - ортогональная матрица, - верхнетреугольная матрица. Далее производится аналогичное разложение для произведения матриц, то есть находятся такие матрицы и что Поскольку матрица ортогональная, легко показать что Повторяя данную процедуру раз приходим к разложению в следующем виде: Поскольку, и -ортогональная а - верхнетреугольные, то локальные показатели Ляпунова (логарифмы собственных чисел матрицы) определяются по следующей формуле: Здесь - - й диагональный элемент матрицы. Оценка показателей Ляпунова по временному ряду с использованием нейронных сетей Алгоритм, описанный в предыдущем разделе, предполагает, что явно задано отображение, определяющее динамическую систему. Однако часто такое отображение не является известным и в распоряжении имеется только наблюдаемый временной ряд. Для того чтобы использовать описанный выше алгоритм достаточно иметь способы оценки матрицы Якоби неизвестного отображения. Это можно сделать различными способами. Первый способ локальный: выбирается область реконструированного аттрактора для оценки матрицы Якоби, производится локальная аппроксимация с использованием соседних точек лежащих на реконструированном аттракторе . Второй способ глобальный. Здесь строится глобальная модель динамической системы: производится аппроксимация отображения задающего динамику системы и затем определяется матрица Якоби для разных точек реконструированного аттрактора. В качестве модели динамической системы удобно брать обученную нейронную сеть прямого распространения как это делалось, например, в . В настоящей работе используется глобальный способ восстановления матриц Якоби. В качестве аппроксиматора используется нейронная сеть с двумя скрытыми слоями. Пусть задан временной ряд. Предполагается, что элементы этого временного ряда являются некоторой наблюдаемой скалярной функцией от состояния динамической системы. Здесь - точки траектории динамической системы, задает нумерацию точек траектории, - отображение задающее эволюцию траектории динамической системы. С помощью стандартной процедуры погружения в лаговое пространство можно перейти к рассмотрению лаговых векторов, где задаются соотношением: Здесь - размерность вложения, - лаг. Можно поставить задачу аппроксимации отображения определяющего динамическую систему: . Поскольку то у отображения неизвестна только последняя компонента. Остальные компоненты задаются как для. Таким образом, задача аппроксимации отображения определяющего динамическую систему: сводится к определению отображения. То есть необходимо аппроксимировать функцию, что можно интерпретировать как задачу прогнозирования временного ряда решаемую методом нелинейной авторегрессии. Подходящей нелинейной моделью аппроксимирующей функцию является нейронная сеть прямого распространения. Мотивацией такому выбору модели является теорема универсальной аппроксимации , которая утверждает, что нейронная сеть с одним скрытым слоем способна со сколь угодной точностью аппроксимировать непрерывную функцию на компактном подмножестве в. Обучающими данными для нейронной сети является набор пар вход-выход задаваемых в виде. Результатом обучения нейронной сети является модель, где - настроенный в процессе обучения вектор весов нейронной сети. Соответствующая модель отображения задается следующим образом: Здесь - -компонента -мерного вектора. Матрица Якоби такой модели определяется по формуле: Согласно теореме Такенса при определенных условиях отображение будет иметь такие же динамические характеристики как и отображение, задающее динамическую систему, которая и порождает временной ряд. Примерами таких характеристик являются фрактальные размерности реконструированного аттрактора, набор обобщенных энтропий и все штук показателей Ляпунова. Таким образом, зная нейросетевую аппроксимацию отображения и имея алгоритм вычисления, можно воспользоваться QR-алгоритмом определения показателей Ляпунова. Полученные показатели будут являться оценкой показателей Ляпунова динамической системы, заданной отображением. Численные эксперименты и результаты Описанный выше алгоритм был протестирован на трёх временных рядах с известными порождающими эти временные ряды динамическими системами. Оценки ГПЛ известны априори. Длина каждого временного ряда - 2000 отсчетов. На рисунке 1 изображены первые 200 отсчетов каждого временного ряда. Ниже перечислены используемые временные ряды, их динамические системы и ГПЛ: 1. logistic - логистическое хаотическое отображение: . ГПЛ равен 2. henon - отображение Хенона. ГПЛ равны, 3. lorenzx - x-компонента системы Лоренца, . ГПЛ равны. Система Лоренца была проинтегрирована с шагом 0,0001 секунд с начальными условиями =0, =1, =1.05 на 2800000 шагов. Первые 1400000 шагов отброшены. Остальные точки (x-компонента) взяты с шагом в 700 шагов (0,07 с). В итоге получился ряд в 2000 отсчетов. Рис.1. Первые 200 отсчетов временных рядов logistic, henon, lorenzx. Для каждого временного ряда был произведен расчет ЛПЛ для от 1 до 200 и для 500 различных начальных точек. Каждый расчет был повторен 30 раз для разных случайных инициализаций весов нейронной сети. Множество обученных сетей образуют комитет нейронных сетей . Как и ожидалось, вне зависимости от начальной точки ЛПЛ сходятся к ГПЛ после 100 шага. На рисунке 2 приведен пример такой сходимости для ряда henon при 10 различных начальных точках. Рис.2. Зависимость и от для 10 различных начальных точек для временного ряда henon. Если зафиксировать =200, то распределение набора значений для каждой сети будет давать некоторый спектр (далее спектр ЛПЛ). Объединённые по 5 лучшим (с наименьшей ошибкой обучения) нейронным сетям спектры ЛПЛ каждого ряда представлены на рисунке 3. Значения ГПЛ помечены на оси абсцисс. Также на рисунке 3 указаны ошибки обучения нейронных сетей. Рис.3. Спектры ЛПЛ (по 5 лучшим нейросетям комитета) временных рядов logistic, henon, lorenzx (слева) и значения среднеквадратичных отклонений (mse) обученных нейросетей (справа). Из рисунков видно, что спектры сосредоточены вблизи априори известных ГПЛ. Среднее значения спектров ЛПЛ можно считать оценкой ГПЛ. Два стандартных отклонения (оценка ширины спектра) можно считать мерой погрешности оценки ГПЛ. Ниже приведена таблица 1 с рассчитанными оценками ГПЛ для 5 лучших сетей комитета и для каждого временного ряда. Также в таблице указаны погрешность, истинные ГПЛ и абсолютная ошибка оценки ГПЛ. Таблица 1 Результаты вычисления ГПЛ ГПЛ Оценка ГПЛ Погрешность Абсолютная ошибка logistic 0.6931 0.6825 0.0164 0.0106 henon 0.41922 0.413 0.032 0.006 -1.62319 -1.609 0.066 0.014 lorenzx 0.9056 1.36 0.64 0.45 0 0.18 0.62 0.18 -14.5723 -15.17 6.80 0.60 Из таблицы 1 видно, что все оценки ГПЛ совпадают с истинными ГПЛ в пределах погрешности (погрешность больше чем допущенная ошибка). Такой результат указывает на работоспособность рассматриваемого метода. Также следует отметить, что оценки старших показателей в пределах погрешности больше 0, что означает, что метод в состоянии определять находится ли изучаемая динамическая система в хаотическом режиме или нет. Заключение Разработанный в работе метод вычисления показателей Ляпунова по временному ряду оказался работоспособным и достаточно точным в случае рассмотренных здесь модельных временных рядов. В дальнейшем планируется применить предложенный здесь метод для анализа временных рядов реального мира. В частности, для финансовых временных рядов с целью определения горизонтов прогнозирования и для временных рядов многоканальных электроэнцефалограмм с целью выявления таких патологий, как эпилепсия.
Динамической системы с непрерывным временем определяют степень отдаления (или сближения) различных, но близких траекторий динамической системы на бесконечности. Если в начале две различных траектории находятся на расстоянии друг от друга, то по прошествии достаточно большого времени расстояние между ними будет выглядеть как:
Где -показатель Ляпунова (англ.)
. Для различных начальных значений числа могут быть различными. Если соответствующий показатель Ляпунова положителен, расстояние между изначально близкими траекториями системы с течением времени увеличивается, если показатель отрицателен - близкие траектории еще более сближаются, наконец, если показатель равен нулю - близкие трактории остаются на примерно одинаковом расстоянии друг от друга. Известно, что для N-мерной динамической системы существует ровно N
показателей Ляпунова ,в общем случае различных (теорема Оселедца (англ.)
, это справедливо для "почти всех" начальных состояний динамической системы). Набор показателей Ляпунова (спектр) характеризует общие закономерности поведения системы для всевозможных начальных условий.

Показатели Ляпунова произвольной динамической системы крайне редко можно получить аналитически (в виде формулы), однако существуют численные методы, которые позволяют вычислять их с приемлемой точностью.
Показатели Ляпунова имеют важное значение в качественной теории динамических систем. Знание показателей Ляпунова позволяет сделать заключение о том, как система развивается с течением времени. Довольно часто достаточно знать ЗНАК старшего, т.е. наибольшего показателя, а также СУММУ показателей.
В трехмерном случае, для систем вида:

если рассматривать только системы, имеющие физический смысл, для которых не все показатели Ляпунова положительны и их сумма неположительна, и обозначить знаком "-" отрицательный показатель Ляпунова, знаком "+" положительный, а знаком "0" - нулевой, то возможны следующие варианты различного поведения:
Для систем более высокой размерности набор вариантов становится более обширным, однако по-прежнему наличие ПОЛОЖИТЕЛЬНОГО показателя Ляпунова (при условии отрицательности их суммы) влечет за собой хаотическое поведениеЧисленное определение показателей Ляпунова
DEREK
умеет вычислять часть спектра показателей Ляпунова (не более 4-х первых показателей, если расположить их в порядке убывания, т.е. для систем не более четвертого порядка определяются ВСЕ показатели), пользуясь численным итерационным алгоритмом Бенеттина (англ.)
. В этом алгоритме показатели Ляпунова находятся с помощью многократного решения вспомогательной динамической системы,которая строится на основании исходной. Для реализации этого алгоритма должны быть заданы начальный шаг по времени (по ), точность решения системы, максимальное количество итераций и точность, с которой будут вычислены показатели Ляпунова. Если заранее известно, что у системы есть нулевой показатель Ляпунова (это справедливо, например, для автономной системы , траектория которой не приближается к неподвижной точке) - можно указать соответствующий признак, это повысит точность расчета.
DEREK
позволяет также вычислить и построить график зависимости нескольких старших показателей Ляпунова от параметра системы. Для построения необходимо задать диапазон изменения параметра и количество шагов, на которые этот диапазон будет разбит. В результате работы будет выведен набор графиков,показывающих зависимость каждого из показателей от параметра (в точках,соответствующих шагам). График может быть составлен из отдельных точек (крупных), соединительных линий или и того, и другого.
Для вычисления показателей Ляпунова с помощью DEREK
а не требуется никакого дополнительного программного обеспечения - ни компиляторов, ни библиотек программ, ни пакетов компютерной алгебры. Кроме того, от пользователя не требуется никаких навыков программирования. Все очень просто - необходимо записать уравнения, определяющие динамическую систему, затем выбрать в меню графического окна системы пункт для вычисления показателей Ляпунова, задать несколько (немного) установочных параметров (или воспользоваться установками по умолчанию). После этого пользователь получает численное значение показателей Ляпунова или графики зависимости показателей от параметра (константы) системы.
Примеры вычисления показателей Ляпунова
Ниже представлены зависимости показателей Ляпунова от параметра системы для некоторых известных динамических систем.
Система Рабиновича-Фабриканта

Модель Мура-Шпигеля

Модель Лоренца

Модель Рёсслера


До сих пор мы рассматривали в основном прогностические критерии хаоса. В этом разделе мы опишем способ, позволяющий диагностировать, находится ли исследуемая система в хаотическом состоянии или нет. Хаос в детерминированных системах подразумевает чувствительную зависимость от начальных условий. Это означает, что две траектории, близкие друг к другу в фазовом пространстве в некоторый начальный момент времени, экспоненциально расходятся за малое в среднем время. Если - мера начального расстояния между двумя исходными точками, то, спустя малое время t, расстояние между траекториями, выходящими из этих точек, становится равным
![]() (5.4.1)
(5.4.1)
Если система описывается разностными уравнениями или отображекием, то
![]() (5.4.2)
(5.4.2)
[Основание 2 выбрано в соотношениях (5.4.1), (5.4.2) из соображений удобства, а в остальном произвольно.] Величины и называются показателями Ляпунова.
Превосходный обзор по показателям Ляпунова и их использованию в экспериментах для диагностики хаотического движения опубликованы Вулфом и др. . В этом же обзоре помещены две полезные компьютерные программы для вычисления показателей Ляпунова.
Экспоненциальная расходимость хаотических траекторий может быть только локальной, так как если система ограниченна (а большинство физических экспериментов ограниченно), то d(t) не может возрастать до бесконечности. Следовательно, для того чтобы определить меру расходимости траекторий, необходимо усреднить экспоненциальный рост по многим точкам вдоль траектории, как показано на рис. 5.26. Вычисление показателя Ляпунова начинается в выбора реперной траектории [Вулф и др. называют ее опорной траекторией], точки на соседней траектории и измерения величины . Когда расстояние d(t) становится слишком большим (т. е. рост его отклоняется от экспоненциального поведения), экспериментатор находит новую «соседнюю» траекторию и определяет новое начальное расстояние .

Рис. 5.26. Общий ход изменения расстояния между двумя соседними траекториям, используемый для определения наибольшего показателя Ляпунова.
Показатель Ляпунова можно задать выражением

Критерий хаоса в терминах показателя Ляпунова принимает следующий вид:
 (5.4.4)
(5.4.4)
Должно быть, читатель уже понял, что без компьютера при вычислении показателя Ляпунова не обойтись ни в том случае, когда данные берутся из численного моделирования, ни в том, когда их источником служит физический эксперимент.
Вычислить в явном виде удается лишь в очень немногочисленных учебных примерах. Рассмотрим один из них, связанный с обобщением понятия «показатель Ляпунова» на одномерные отображения:
![]() (5.4.5)
(5.4.5)
Там, где функция гладкая и дифференцируемая, расстояние между соседними траекториями измеряется величиной . Чтобы убедиться в этом, введем два начальных условия: . Тогда в соотношении (5.4.2)

Следуя соотношению (5.4.3), определить показатель Ляпунова (или характеристический показатель) как

В качестве иллюстративного примера воспользуемся отображением Бернулли
(рис. 5.27). Здесь (mod 1) означает дробную часть, т. е.

Рис. 5.27. Хаотическая траектория при отображении Бернулли .
Это отображение многозначно и, как известно, рождает хаос. За исключением разрыва в точке х = 1/2, всюду в остальных точках . Из определения (5.4.7) получаем . Следовательно, в среднем расстояние между соседними точками растет как
![]()
Единицами измерения показателя Ляпунова служат биты на одну итерацию. Одна из интерпретаций состоит в том, что при каждой итерации отображения теряется битов информации о начальном состоянии. Чтобы убедиться в этом, запишем в двоичной системе. Например, означает . Таким образом, отображение сдвигает запятую на один знак вправо и отбрасывает целую часть. Следовательно, если мы начинаем с значащих знаков после запятой, то при каждой итерации теряем по одному, т. е. теряем по одному биту информации.
После итераций мы полностью утрачиваем информацию о начальном состоянии системы.
Ранее в этой главе мы узнали, что логистическое, или квадратичное, отображение становится хаотическим, когда управляющий параметр .
Читайте также...
- Курсовая работа: Колебательные химические реакции Исследования концентрационных колебаний до открытия реакции Белоусовым
- Английские слова для изучения на каждый день: полезная лексика и советы для запоминания
- Публичное выступление: интересные примеры
- Сетевая викторина «Когда Россия молодая мужала с гением Петра